Chapter 2: Investment appraisal – methods incorporating the use of free cash flows
Chapter learning Objectives
Upon completion of this chapter you will be able to:
- define and calculate basic free cash flows for a specified capital investment project
- calculate free cash flows for a specified capital investment project incorporating general inflation and specific price variation
- calculate free cash flows for a specified capital investment project incorporating taxation and consider the potential impact of changes in tax rates
- prepare a basic linear programming formulation consisting of named variables, an objective function and a series of constraints
- define multi-period capital rationing
- prepare an NPV linear programming formulation to deal with a multi-period capital rationing problem
- interpret output provided resulting from a NPV linear programming formulation
- prepare a PV of dividends linear programming formulation to deal with a multi-period capital rationing problem
- interpret output provided resulting from an PV of dividends linear programming formulation
- calculate the economic return of a specified capital investment project by calculating the IRR
- use the IRR of a specified capital investment project to advise on a project’s return margin
- calculate the economic return of a specified capital investment project by calculating the modified IRR

1 Free cash flows
 Cash that is not retained and reinvested in the business is called free cash flow.
Cash that is not retained and reinvested in the business is called free cash flow.
It represents cash flow available:
- to all the providers of capital of a company
- to pay dividends or finance additional capital projects.
Uses of free cash flows
Free cash flows are used frequently in financial management:
- as a basis for evaluating potential investment projects - see below
- as an indicator of company performance - see Chapter 11
- to calculate the value of a firm and thus a potential share price - see Chapter 10.
Calculating free cash flows for investment appraisal
Free cash flows can be calculated simply as:
Free cash flow = Revenue - Costs - Investments
The free cash flows used to evaluate investment projects are therefore essentially the net relevant cash flows you will recall from your earlier studies.
Use of free cash flows in investment appraisal
This chapter covers the following investment appraisal methods, all of which incorporate the use of free cash flows:
- Net Present Value (NPV)
- Internal Rate Of Return (IRR)
- Modified Internal Rate Of Return (MIRR)
- Discounted Payback Period
- Duration (Macauley Duration)
2 Net Present Value
Capital investment projects are best evaluated using the netpresent value (NPV) technique. You should recall from earlier studiesthat this involved discounting the relevant cash flows for each year of the project at an appropriate cost of capital.
As mentioned above the net relevant cash flows associated with theproject are the free cash flows it generates. The discounted free cashflows are totalled to provide the NPV of the project.
Some basic NPV concepts are revised as follows:
Relevant costs and revenues
Relevant flows are those costs and revenues, which are:
Some basic NPV concepts are revised as follows:
You should therefore ignore:
- sunk costs
- committed costs
- non-cash items
- apportioned overheads.
Discounting
The impact of inflation
The treatment of inflation was introduced in Paper F9. A brief recap follows:
Inflation is a general increase in prices leading to a general decline in the real value of money.
In times of inflation, the fund providers will require a return made up of two elements:
- Real return for the use of their funds.
- Additional return to compensate for inflation.
The overall required return is called the money or nominal rate of return.
Real and nominal rates are linked by the formula:

in which :

In investment appraisal two types of inflation need consideration:
This inflationary impact can be dealt with in two different ways – both methods give the same NPV.
Note:
- as stated above, the real method can only be used if all cash flows are inflating at the general rate of inflation.
- in questions involving specific inflation rates, taxation or working capital, the money / nominal method is usually more reliable.
Calculating the free cash flows of a project under inflation
In project appraisal the impact of inflation must therefore betaken into account when calculating the free cash flows to bediscounted.

 Illustration: Inflation in investment appraisal
Illustration: Inflation in investment appraisal
A company is considering investing $4.5m in a project to achieve an annual increase in revenues over the next five years of $2m.
The project will lead to an increase in wage costs of $0.4m pa andwill also require expenditure of $0.3m pa to maintain the level ofexisting assets to be used on the project.
Additional investment in working capital equivalent to 10% of theincrease in revenue will need to be in place at the start of each year.
The following forecasts are made of the rates of inflation each year for the next five years:

The real cost of capital of the company is 8%.
All cash flows are in real terms. Ignore tax.
Find the free cash flows of the project and determine whether it is worthwhile.
Solution

The NPV = $1,389,000 which suggests that the project is worthwhile.
W1 working capital injection

W2 cost of capital
(1 + i) = (1 + r) (1 + h) = (1.08) (1.065) = 1.15, giving i = 15%


 Test your understanding 1
Test your understanding 1
A company plans to invest $7m in a new product. Net contribution overthe next five years is expected to be $4.2m pa in real terms.
Marketing expenditure of $1.4m pa will also be needed.
Expenditure of $1.3m pa will be required to replace existing assetswhich will now be used on the project but are getting to the end oftheir useful lives. This expenditure will be incurred at the start ofeach year.
Additional investment in working capital equivalent to 10% ofcontribution will need to be in place at the start of each year. Workingcapital will be released at the end of the project.
The following forecasts are made of the rates of inflation each year for the next five years:

The real cost of capital of the company is 6%.
All cash flows are in real terms. Ignore tax.
Find the free cash flows of the project and determine whether it is worthwhile.

The impact of taxation
The treatment of taxation was also introduced in Paper F9. There are two main impacts of taxation in an investment appraisal:
- tax is charged on operating cashflows, and
- tax allowable depreciation / capital allowances / writing down allowances can be claimed, thus generating tax relief

 Revision of taxation on operating cashflows
Revision of taxation on operating cashflows
Tax on operating flows
Corporation tax charged on a company’s profits is a relevant cash flow for NPV purposes. It is assumed that:
- operating cash inflows will be taxed at the corporation tax rate
- operating cash outflows will be tax deductible and attract tax relief at the corporation tax rate
- tax is paid in the same year the related operating cash flow is earned unless otherwise stated
- investment spending attracts capital or writing down allowances which get tax relief (see the section below)
- the company is earning net taxable profits overall.


 Revision of Tax Allowable Depreciation
Revision of Tax Allowable Depreciation
Tax allowable depreciation / Capital allowances / writing down allowances (WDAs)
For tax purposes, a business may not deduct the cost of an assetfrom its profits as depreciation (in the way it does for financialaccounting purposes). Instead the cost must be deducted in the form oftax allowable depreciation or writing down allowances (WDAs).
The basic rules that follow are based on the current UK tax legislation:
- Writing down allowances are calculated on a reducing balance basis (usually at a rate of 25%).
- The total WDAs given over the life of an asset equate to their fall in value over the period (i.e. the cost less any scrap proceeds).
- Writing down allowances are claimed as early as possible.
- WDAs are given for every year of ownership except the year of disposal.
- In the year of sale or scrap a balancing allowance or charge arises.

You should carefully check the information given in the questionhowever, since the examiner could ask you to examine the impact on theproject of potential changes in the rules, for example:
- giving a 50% WDA in the first year of ownership and 25% thereafter
- giving 100% first year allowances (these are sometimes available to encourage investment in certain areas or types of assets)
- changing the calculation method from reducing balance to straight line.

Calculating the free cash flows of a project taking account of taxation
In project appraisal the effects of taxation must be taken into account when calculating the free cash flows to be discounted.

 Illustration: Taxation in investment appraisal
Illustration: Taxation in investment appraisal
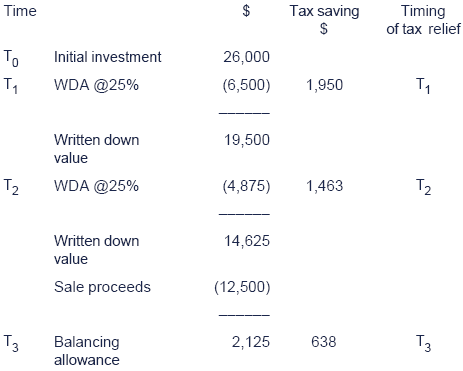
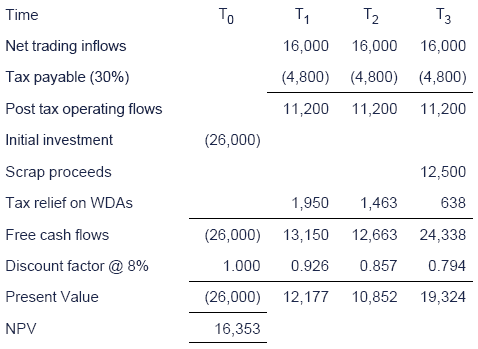
A company buys an asset for $26,000. It will be used on a projectfor three years after which it will be disposed of on the final day ofyear 3. Tax is payable at 30% and capital allowances are available at25% reducing balance.
A Calculate the writing down allowance and hence the tax savings foreach year if the proceeds on disposal of the asset are $12,500.
B If net trading income from the project is $16,000 pa and the cost ofcapital is 8% calculate the free cash flows and hence the net presentvalue (NPV) of the project.
Solution


 Test your understanding 2
Test your understanding 2
A project will require an investment in a new asset of $10,000. Itwill be used on a project for four years after which it will be disposedof on the final day of year 4. Tax is payable at 30% one year inarrears, and capital allowances are available at 25% reducing balance.
Net operating flows from the project are expected to be $4,000 pa.
The company’s cost of capital is 10%. Ignore inflation.
A Calculate the writing downallowance and hence the tax savings for each year if the proceeds ondisposal of the asset are $2,500.
B Identify the free cash flows for the project and calculate its net present value (NPV).

3 The Internal Rate of Return (IRR)
As well as NPV, the other discounting technique used to appraiseinvestment projects, which you should recall from earlier studies, isthe calculation of the internal rate of return or the IRR.
A brief recap follows:
IRR – the basics
The IRR of a project has the following features:
- It represents the discount rate at which the NPV of an investment is zero.
- It can be found by linear interpolation.
- Standard projects (outflow followed by inflows) should be accepted if the IRR is greater than the firm’s cost of capital.
The steps in linear interpolation are:
(1) Calculate two NPVs for the project at two different costs of capital.
(2) Use the following formula to find the IRR:
where:
L = Lower rate of interest.
H = Higher rate of interest.
NL = NPV at lower rate of interest.
NH = NPV at higher rate of interest.
(3) Compare the IRR with the company’s cost of borrowing.
If the IRR is higher than the cost of capital, the project should be accepted.

 Test your understanding 3
Test your understanding 3
An initial investment of $2,000 in a project yields cash inflows of$500, $500, $600, $600 and $440 at 12 months intervals. There is noscrap value. Funds are available to finance the project at 12%.
Decide whether the project is worthwhile, using:
A net present value approach
B internal rate of return approach.

Interpreting the IRR
The IRR provides a decision rule for investment appraisal, but alsoprovides information about the riskiness of a project – i.e. thesensitivity of its returns.
The project will only continue to have a positive NPV whilst the firm’s cost of capital is lower than the IRR.
A project with a positive NPV at 14% but an IRR of 15% for example, is clearly sensitive to:
- an increase in the cost of finance
- an increase in investors’ perception of the potential risks
- any alteration to the estimates used in the NPV appraisal.

 Interpretation of IRR
Interpretation of IRR
Increases in interest rates will clearly increase the company’scosts of finance as will concerns affecting the stock market as a wholeand hence the returns demanded by investors.
However, other, company specific factors – such as the actions ofcompetitors may affect the firm’s position in the market place andthe viability of its business model. This could impact the level ofsystematic risk it faces and result in an increase in the requiredreturn of shareholders.
Where the IRR is close to the company cost of capital, any changesto estimates in the NPV calculation will have a significant impact onthe viability of the project. Any unexpected changes such as an increasein the costs of raw materials, or an aggressive advertising campaignrun by a competitor will erode the return margin and may make theproject unacceptable to investors.

4 The modified IRR (MIRR)
Problems with using IRR
There are a number of problems with the standard IRR calculation:
- The decision rule is not always clear cut. For example, if a project has 2 IRRs (or more), it is difficult to interpret the rule which says "accept the project if the IRR is higher than the cost of capital".
- The assumptions. IRR is often mistakenly assumed to be a measure of the return from a project, which it is not. The IRR only represents the return from the project if funds can be reinvested at the IRR for the duration of the project.
- Choosing between projects. Since projects can have multiple IRRs (or none at all) it is difficult to usefully compare projects using IRR.
It is therefore usually considered more reliable to calculate the NPV of projects for investment appraisal purposes.

 More on the problems with IRR
More on the problems with IRR
For conventional projects (those with a cash outflow at time 0followed by inflows over the life of the project), the decision rulestates that projects should be accepted if the IRR exceeds the cost ofcapital.
However unconventional projects with different cash flow patternsmay have no IRR, more than one IRR, or a single IRR but the projectshould only be accepted if the cost of capital is greater.
The IRR calculates the discount rate that would cause the project to break-even assuming it:
- is the cost of financing the project
- is the return that can be earned on all the returns earned by the project.
Since, in practice, these rates are likely to be different, the IRR is unreliable.
A project with a high IRR is not necessarily the one offering thehighest return in NPV terms and IRR is therefore an unreliable tool forchoosing between mutually exclusive projects.

A more useful measure is the modified internal rate of return or MIRR.
This measure has been developed to counter the above problems since it:
- is unique
- can deal with different borrowing and reinvestment rates
- is a simple percentage.
It is therefore more popular with non-financially minded managers, as a simple rule can be applied:
The interpretation of MIRR
MIRR measures the economic yield of the investment under theassumption that any cash surpluses are reinvested at the firm’scurrent cost of capital.
Although MIRR, like IRR, cannot replace net present value as theprinciple evaluation technique it does give a measure of the maximumcost of finance that the firm could sustain and allow the project toremain worthwhile. For this reason it gives a useful insight into themargin of error, or room for negotiation, when considering the financingof particular investment projects.
Calculating the MIRR
Method:
(1) Find the terminal value of the cash inflows from the project if invested at the company's reinvestment rate.
(2) Find the present value of the cash outflows, discounted at the company's cost of finance.
(3) The MIRR is then found bytaking the n th root of (TV inflows / PV outflows) and subtracting 1(Note that n is the length of the project in years.)
Student Accountant article
Read Bob Ryan's April 2008 article in Student Accountant magazine for more details on MIRR.

 Illustration of NPV, IRR and MIRR
Illustration of NPV, IRR and MIRR
A project requires an initial investment of $24,000 and will generate annual cash flows as follows:

The cost of capital is 10%.
A Find the NPV and the IRR of the project.
B Show the overall net cash position for the project if:
- the company had a cost of capital equivalent to the IRR
- and all cash flows earned were invested for the duration of the project at that rate.
C Assume now that funds can be borrowed at 10% whilst the reinvestment rate for positive cash flows is 12%. What is the MIRR?
Solution
NPV

IRR

This gives an IRR of:
IRR = 10 + [1,967.8/(1,967.8 - 555.8)] × (14 - 4) = 13.12%
Using a spreadsheet a more accurate IRR can be shown to be 13.07% and it is this will use for demonstration purpose:
Net cash position

Total amount invested at end of project. The time 5 value of the cost of the investment: $24,000 × (1.1307)5 = $44,356 which matches the value of the income from the returns.
Or alternatively
Time 0 value of the income from the returns = 44,360/1.13075 = $24,002 which matches the initial cost of the project.
The net cash position for the project is therefore effectively zero– i.e. an IRR of 13.07% means that if the cost of borrowing and thereturn earned on investments were both 13.07%, the project would breakeven.
MIRR
To calculate the MIRR, we restate the project cash flows to beequivalent to an outflow at time 0 and a single inflow at the end of theproject life (the ‘terminal value’), using the assumed reinvestmentrate.
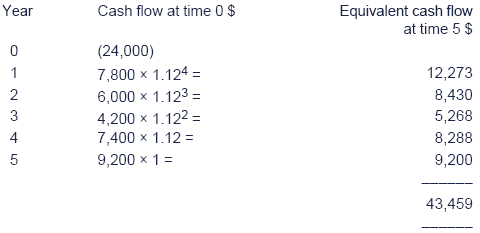
Thus, what is the IRR of a cash outflow of $24,000 at time 0 followed by an inflow of $43,459 at time 5?
43,459/(1 + r)5 = 24,000
43,459/24,000 = (1 + r)5

r = 0.126
so the MIRR is 12.6%. This is therefore the return on the project.
Since the return on the project exceeds the cost of finance, the project should be accepted.


 Test your understanding 4
Test your understanding 4
A project requires an initial investment of $20,000 and will generate annual cash flows as follows:

The firm's financing rate (for negative cashflows) is 9%, and its reinvestment rate for positive cashflows is 6%.
What is the MIRR?

Alternative calculation of MIRR
To avoid having to calculate the terminal value of the projectinflows, there is an alternative way of computing MIRR which only usespresent value calculations.
1 + MIRR = (1+re) × [PVR/PVI]1/n
where
PVR = the present value of the "return phase" of the project
PVI = the present value of the "investment phase" of the project
re = the firm's cost of capital
This formula is given on the exam formula sheet.

 Illustration 1: MIRR
Illustration 1: MIRR
A project with the following cash flows is under consideration:
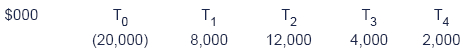
Cost of capital 8%
Required:
Calculate the MIRR.
Solution
PVR = 22,340 (this is the present value of the year 1-4 cash flows).
PVI = 20,000
1 + MIRR = (1+re) × (PVR/PVI)1/n = 1.08 × (22,340/20,000)1/4 = 1.1103, giving MIRR = 11% pa.
Check: MIRR calculated the “long wayâ€:
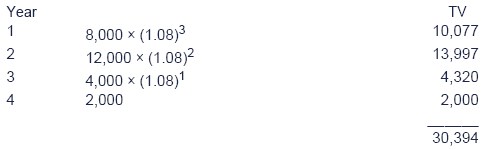
1 + MIRR = (30,394/20,000)1/4 = 1.1103, as before

5 Discounted Payback Period (DPP)
Traditional payback period
The payback period was introduced in paper F9.
Payback period measures the length of time it takes for the cash returns from a project to cover the initial investment.
The main problem with payback period is that it does not take account of the time value of money.
Discounted payback period
Hence, the discounted payback period can be computed instead.
Discounted payback period measures the length of time before thediscounted cash returns from a project cover the initial investment.
The shorter the discounted payback period, the more attractive theproject is. A long discounted payback period indicates that the projectis a high risk project.

 Illustration 2: Discounted Payback Period
Illustration 2: Discounted Payback Period
A project with the following cash flows is under consideration:
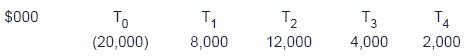
Cost of capital 8%
Required:
Calculate the Discounted Payback Period.
Solution


6 Duration (Macauley duration)
Introduction to the concept of duration
Duration measures the average time to recover the present value ofthe project (if cash flows are discounted at the cost of capital).
Duration captures both the time value of money and the whole of thecash flows of a project. It is also a measure which can be used acrossprojects to indicate when the bulk of the project value will becaptured.
Projects with higher durations carry more risk than projects with lower durations.
Calculation of duration
There are several different ways of calculating duration, the most common of which is Macauley duration, illustrated below.

 More details on duration
More details on duration
As mentioned above, duration measures the average time to recoverthe present value of the project if discounted at the cost of capital.
However, if cashflows are discounted at the project's IRR, it can be used to measure the time to recover the initial investment.
As well as being used in project appraisal, duration is commonlyused to assess the likely volatility (risk) associated with corporatebonds. An example of duration in the context of bonds is shown inChapter 3.


 Payback, Discounted Payback and Duration
Payback, Discounted Payback and Duration
Payback, discounted payback and duration are three techniques that measure the return to liquidity offered by a capital project.
In theory, a firm that has ready access to the capital marketsshould not be concerned about the time taken to recapture the investmentin a project. However, in practice managers prefer projects to appearto be successful as quickly as possible.
Payback period
Payback as a technique fails to take into account the time value ofmoney and any cash flows beyond the project date. It is used by manyfirms as a coarse filter of projects and it has been suggested to be aproxy for the redeployment real option.
Discounted payback period
Discounted payback does surmount the first difficulty but not thesecond in that it is still possible for projects with highly negativeterminal cash flows to appear attractive because of their initialfavourable cash flows. Conversely, discounted payback may lead a projectto be discarded that has highly favourable cash flows after the paybackdate.
Duration
Duration measures either the average time to recover the initialinvestment (if discounted at the project’s internal rate of return) ofa project, or to recover the present value of the project if discountedat the cost of capital. Duration captures both the time value of moneyand the whole of the cash flows of a project. It is also a measure whichcan be used across projects to indicate when the bulk of the projectvalue will be captured.
Its disadvantage is that it is more difficult to conceptualise than payback and may not be employed for that reason.


 Illustration 3: Macauley duration
Illustration 3: Macauley duration
A project with the following cash flows is under consideration:
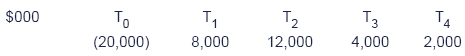
Cost of capital 8%
Required:
Calculate the project's Macauley duration.
Solution
The Macauley duration is calculated by first calculating thediscounted cash flow for each future year, and then weighting eachdiscounted cash flow according to its time of receipt, as follows:

Next, the sum of the (PV × Year) figures is found, and divided by the present value of these "return phase" cash flows.
Sum of (PV × Year) figures = 7,408 + 20,568 + 9,528 + 5,880 = 43,384
Present value of return phase cash flows = 7,408 + 10,284 + 3,176 + 1,470 = 22,338
Hence, the Macauley duration is 43,384 / 22,338 = 1.94 years


 Test your understanding 5
Test your understanding 5
A project with the following cash flows is under consideration:
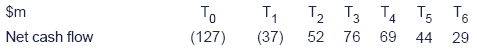
Cost of capital 10%
Required:
Calculate the project's discounted payback period and Macauley duration.

7 Investment appraisal and capital rationing
Capital rationing was first introduced in Paper F9. A brief recap follows:
Capital rationing – the basics
Shareholder wealth is maximised if a company undertakes all possible positive NPV projects.
Capital rationing is where there are insufficient funds to do so.
This shortage of funds may be for:

 Test your understanding 6
Test your understanding 6
Peel Co has identified 4 positive NPV projects, as follows:

Peel Co can only raise $12m of finance to invest at t0.
Advise the company which project(s) to accept if the projects are:
(i)independent and divisible
(ii) independent and indivisible
(iii)mutually exclusive

Multi-period capital rationing
A solution to a multi-period capital rationing problem cannot befound using PIs. This method can only deal with one limiting factor(i.e. one period of shortage). Here there are a number of limitingfactors (i.e. a number of periods of shortage) and linear programmingtechniques must therefore be applied.
In the exam you will not be expected to produce a solutionto a linear programming problem. However, in the followingillustrations, you will see how to formulate a linear programming model.
In practice, long term capital rationing is a signal that the firmshould be looking to expand its capital base through a new issue offinance to the markets.

 Revision of linear programming
Revision of linear programming
In your previous studies, (Papers F2 and F5), you were introducedto the details of linear programming. In this paper, we are interestedonly in formulating the linear programming problem and this revisionexample therefore only reviews those first key stages.
Linear programming is a technique for dealing with scarce orrationed resources. The solution calculated identifies the optimumallocation of the scarce resources between the products/projects beingconsidered.
A brief recap follows:
The linear programme is formulated in three stages:
(1) Define the unknowns.
(2) Formulate the objective function.
(3) Express the constraints in terms of inequalities including the non-negativities.


 Simple Linear Programming Example
Simple Linear Programming Example
A company makes two products, brooms and mops. Each product passesthrough two departments, manufacture and packaging. The time spent ineach department is as follows:

There are 4,800 hours available in the manufacturing department and3,600 available in the packaging department. Production of brooms mustnot exceed 1,100 units.
The contribution earned from one broom is $15 and from a mop is $10.
Formulate the linear programme needed to identify the optimum use of the scarce labour resource.
Solution
(1) Define the unknowns
Let m = number of mops to be produced.
Let b = number of brooms to be produced.
Let z = contribution earned from the products made.
(2) Formulate the objective function
The aim is to maximise contribution:
z = 15b + 10m.
(3) Express the constraints in terms of inequalities including the non-negativities
The main constraints simply say that you cannot use any more of the resource than you have available.
Since only 4,800 hours of manufacturing time is available, theconstraint shows that the number of hours taken to make a broom timesthe number of brooms made (3b) plus the number of hours needed to make amop times the number of mops made (4m) must not exceed 4,800.
The same principle is applied to packaging time.
The third constraint restricts the production of brooms to 1,100.
The non-negative constraints at the end, prevent negativequantities from being produced. (If this seems unnecessary, rememberthat a computer solving the problem does not have a sense of this beingridiculous and producing negative quantities would, on paper, actuallycontribute scarce resource!)

The linear programming method can be applied to a multi-periodcapital rationing problem in one of two ways. The objective of thesolution can be either:
- to maximise the total NPV from the investment in available projects
- to maximise the present value of cash flow available for dividends.
Both techniques result in the same project selections.

 Example of the NPV formulation
Example of the NPV formulation
A company has identified the following independent investmentprojects, all of which are divisible and exhibit constant returns toscale. No project can be delayed or done more than once.
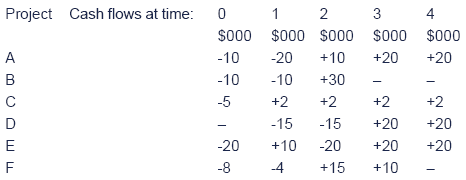
There is only $20,000 of capital available at T0 and only $5,000 at T1, plus the cash inflows from the projects undertaken at T0. In each time period thereafter, capital is freely available. The appropriate discount rate is 10%.
Formulate the NPV linear programme.
Solution
Since our objective is to maximise the total NPV from theinvestments the first (additional) stage will be to calculate those NPVsat a discount rate of 10%.

We now progress as for a standard linear programme:
(1) Define the unknowns
The linear programme will then select the combination of projects, which will maximise total NPV.
Therefore:
Let a = the proportion of project A undertaken
Let b = the proportion of project B undertaken
Let c = the proportion of project C undertaken
Let d = the proportion of project D undertaken
Let e = the proportion of project E undertaken
Let f = the proportion of project F undertaken
And
Let z = the NPV of the combination of projects selected.
(2) Formulate the objective function
The objective function to be maximised is:
z = 8.77a + 5.70b + 1.34c + 2.65d + 1.25e + 8.27f.
(3) Express the constraints in terms of inequalities including the non-negativities
(4) Interpret the results
The linear programme when solved will give values for a, b, c, d, eand f. These will be the proportions of each project which, should beundertaken to maximise the NPV – an amount given by z.
Further details on interpretation
The objective function (z) is the maximum NPV earned. This willbe the sum of the NPVs earned from each product. Since they may each bedone only in part, the full NPV from each one is multiplied by theproportion of it to be undertaken (a, b, c etc.) and these are thensummed together to give the objective function.
The main constraints simply say that you cannot spend any more money than you have available.
- The first constraint relates to the limited capital available at T0.
- How much of the T0 capital for each project will actually be needed, depends on the proportions of each project undertaken. The full T0 amounts are therefore multiplied by the proportions to be undertaken, and the sum of those amounts must not exceed the $20,000 available.
- The second constraint relates to the limited capital available at T1.
- Here the financial situation is eased because projects C and E have positive cash inflows at T1 and these flows can be used to fund investment needs at that time.
- The funds required by projects using limited cash (A, B, D, and F) are therefore multiplied by the proportions to be undertaken. This amount must be less than what is available – the $5,000 plus the funds brought it by whatever proportions of C and E we end up choosing to do.
The third constraint is a summarised one. It shows that none of theprojects can be done more than once (i.e. must be ≤1) and that is notpossible to do a negative amount of any project (they must be ≥ 0).This second non-negative rule is essential. If it were not included, acomputer model may well compute that effectively ‘undoing’ a projectfrees up cash and include it in a solution!


 Example of the PV of dividends formulation
Example of the PV of dividends formulation
Linear programming and capital rationing – the PV of dividends formulation
This method is more flexible and removes the need to calculate theNPVs of the projects as this is taken care of by the linear programmeitself.
The objective is to maximise the cash flows for dividends during the life span of the available projects.
The same information will be used as for the last example in order to provide a clear comparison.
Example
A company has identified the following independent investmentprojects, all of which are divisible and exhibit constant returns toscale. No project can be done more than once.
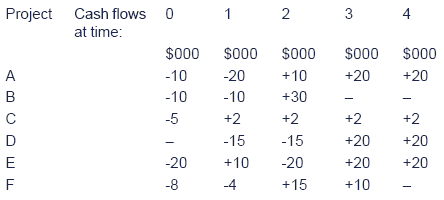
There is only $20,000 of capital available at T0 and only $5,000 at T1, plus the cash inflows from the projects undertaken at T0. In each time period thereafter, capital is freely available. The appropriate discount rate is 10%.
Formulate the PV of dividends linear programme.
Solution
(1) Define the unknowns
As before the amount of each project to be undertaken is shown as:
Let a = the proportion of project A undertaken.
Let b = the proportion of project B undertaken.
Let c = the proportion of project C undertaken.
Let d = the proportion of project D undertaken.
Let e = the proportion of project E undertaken.
Let f = the proportion of project F undertaken.
But for the objective function:
Let z = the PV of dividends.
In addition, the dividend flows must be defined:
Let d0 = dividend flow generated at T0 by the projects selected.
Let d1 = dividend flow generated at T1 by the projects selected.
Let d2 = dividend flow generated at T2 by the projects selected.
Let d3 = dividend flow generated at T3 by the projects selected.
Let d4 = dividend flow generated at T4 by the projects selected.
(2) Formulate the objective function
The objective function to be maximised is:
z = d0/1+ d1/1.1+ d2/1.12+ d3/1.13+ d4/1.14
or
z = d0 + 0.909 d1 + 0.826 d2 + 0.751 d3 + 0.683 d4
(3) Express the constraints in terms of inequalities including the non-negativities
(4) Interpret the results
The linear programme when solved will give values for a, b, c, d, e and f.
These will be the proportions of each project, which should beundertaken to maximise the PV of dividends – an amount given by z.
Note that the only difference in the value of z in these formulations is:
- PV of dividends formulation – z gives the PV of the project returns gross of the investment cost.
- NPV formulation – z gives the PV of the project returns net of the investment cost.
Note that the dividend flows are defined for each of theperiods in which there are projects under consideration. Where theprojects are for varying durations, the flows are defined for each yearup to the point where the cash flow from the longest-lived investmentopportunity stops.
The cost of capital is 10%. Since it is the present value ofdividends to be maximised, the cash flow for each year is discounted at10%. The first version shows z using the formula to give the presentvalue of each year. The second version uses the discount factors fromthe formula sheets.
As before the main constraints express the fact that we cannot spend more than we have.
Whilst for an NPV formulation, we will have as only as manymain constraints as there are periods of capital rationing, in the PV ofdividends formulation we need a constraint for every year for which wehave potential project cash flows.
As before, the outflows include the funds required for theprojects, but now also include the dividend flow for the period. Theavailable funds are as before – the cash supplied by the company plusany income from the projects.
Therefore:
- The first two constraints are amended to include the dividend flow as an additional payment to be funded.
- Then, further constraints are formulated for the remaining three years.
The additional constraint, for the proportion of the projectsto be undertaken, is as before, but we now need an additionalnon-negative constraint – the dividends cannot be negative amounts –they must exceed or equal zero. Again, if it seems unnecessary,consider a computer program solving the formulation – if permitted, itmay indeed make the dividend payments negative, as they would representincome and fund more projects!

Dual values
Dual values are the change in the objective function from having one more or less unit of scarce resource available.
In capital rationing, the scarce resource is cash and dual values can be used to calculate:
- the impact of raising funds to facilitate further investment or
- diverting funds away from current projects to newly discovered ones.
Dual values can be used to filter newly discovered investmentprojects. The cash flows they would generate can be compared with theimpact of diverting funds away from the current investment plan. Thedual values can be used quickly to calculate the effect of diverting thefunds.

 More on dual values
More on dual values
The dual price is:
- the amount by which one additional unit of scarce resource would increase the value of the objective function, or alternatively
- the amount by which one fewer unit of scarce resource would decrease the value of the objective function.
In capital rationing, the scarce resource is available funds, sothe dual value expresses the increase in the objective function gainedif one more dollar became available, or the reduction if one less dollarwere invested.
The amount of the dual value varies depending on which method is used to formulate the linear programme:
- NPV method – the dual equals the change in NPV earned if $1 more or less is available.
- PV of dividends method – the dual equals the change in the PV of cash available to pay dividends if $1 more or less is available.
An example is given here for clarity.
A company under capital rationing has developed an investment planusing linear programming. It has a cost of capital of 10%. The dualvalues have been calculated as:
- NPV method: T0 = 0.2, T1 = 0.07, T2 = 0.
- PV of dividends method: T0 = 1.2, T1 = 0.979,T2 = 0.826.
A new project has come to light with the following flows:

Appraisal using NPV duals
(1) Calculate the NPV of the new project

(2) Find dual value of the project – i.e. the impact on the current investment plan of diverting funds

The NPV of the current investment plan would therefore fall by $4,600 if the new project were taken on.
(3)Compare the two

The project is therefore worthy of further consideration as it should increase the overall NPV of the investments by $100.
Appraisal using PV of dividend duals
This method is far simpler but will always give the same result.

The increase in funds will be $100 as before.

8 The impact of corporate reporting on investment appraisal
The main approach to evaluating capital investment projects andfinancing options, for a profit-maximiser, is their impact onshareholder value. However, the impact on the reported financialposition and performance of the firm must also be considered. Inparticular, you may need to examine the implications for:
- the share price
- gearing
- ROCE
- earning per share.
Timing differences between cash flows and profits
For NPV purposes, the timing of the cash flows associated with aproject is taken account of through the discounting process. It istherefore irrelevant if the cash flows in the earlier years arenegative, provided overall the present value of the cash inflowsoutweighs the costs.
However, the impact on reported profits may be significant. Majornew investment will bring about higher levels of depreciation in theearlier years, which are not yet matched by higher revenues. This willreduce reported profits and the EPS figure.
This reduction could impact:
- the share price – if the reasons for the fall in profit are not understood
- key ratios such as:
- ROCE
- asset turnover
- profit margins.
- the meeting of loan covenants.
9 Chapter summary
Test your understanding answers

 Test your understanding 1
Test your understanding 1
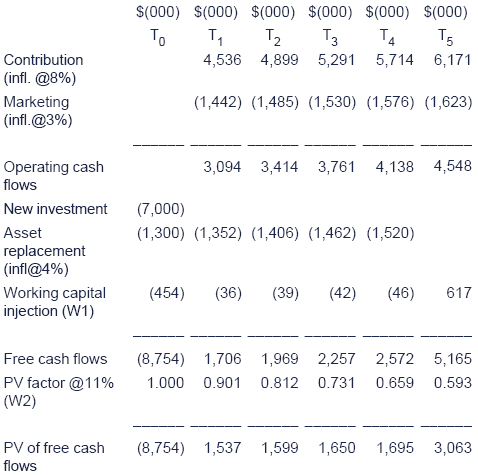
The NPV = +$790,000 which suggests that the project is worthwhile.
W1 Working capital injection

W2 Cost of capital
(1 + i) = (1 + r) (1 + h) = (1 + 0.06) (1 + 0.047) = 1.11, giving i = 11%


 Test your understanding 2
Test your understanding 2
(a)

Note
- total WDAs = 2,500 + 1,875 + 1,406 + 1,719 = 7,500 = fall in value of the asset
- total tax relief = 750 + 563 + 422 + 516 = 2251 = 7,500 × 30%
(b)
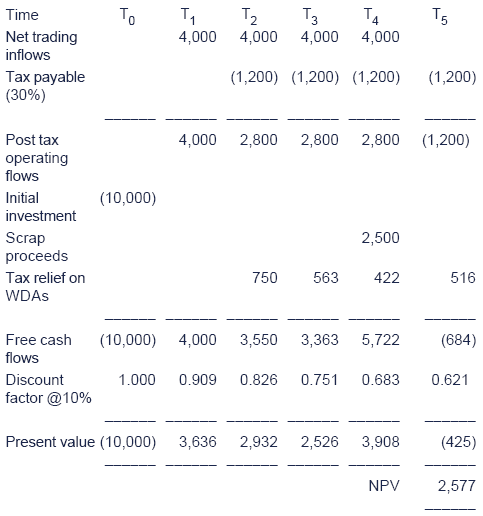


 Test your understanding 3
Test your understanding 3
It is useful to set out the cash flows in a table:
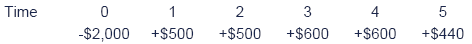
A Net present value approach

Since the net present value at 12% is negative, the project should be rejected.
B Internal rate of return approach
Calculating IRR requires a trial and error approach. Since we havealready calculated in (a) that NPV at 12% is negative, we must decreasethe discount rate to bring the NPV towards zero – try 8%.

See above: NPV is +$108.
Thus, the IRR lies between 8% and 12%. We may estimate it by interpolation, as before.
IRR = 8% +[108/(108 - (-98))] × (12% - 8%)
= 10.1%
The project should be rejected because the IRR is less than thecost of borrowing, which is 12%, i.e. the same conclusion as with NPVanalysis above.


 Test your understanding 4
Test your understanding 4

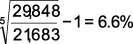
Since the MIRR, the return on the project, is less than the cost of finance, the project should be rejected.


 Test your understanding 5
Test your understanding 5
Workings:

Discounted payback period
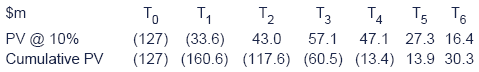
So discounted payback period = 4 years + (13.4 / 27.3) = 4.5 years
Duration

So duration = (86.0 + 171.3 + 188.4 + 136.5 +98.4) / (43.0 + 57.1 + 47.1 + 27.3 + 16.4)
= 680.6 / 190.9
= 3.6 years


 Test your understanding 6
Test your understanding 6
(i)When projects are independent and divisible, the PI method can be used.
So, first do Project A (cost $9m), then do half of project C (cost $6m / 2 = $3m) to use the $12m of capital.
Total NPV = $60m (from A) + $17.5m (from half of C) = $77.5m
(ii) If projects are indivisible, a trial and error approach has to be used.
Choices for $12m investment are:
Either do A, or B, or (C+D).
By inspection, the best option is A, with an NPV of $60m.
(iii)If projects are mutually exclusive, pick the one with the highest positive NPV, i.e. A, with an NPV of $60m.

|
Created at 5/24/2012 3:50 PM by System Account
(GMT) Greenwich Mean Time : Dublin, Edinburgh, Lisbon, London
|
Last modified at 5/25/2012 12:55 PM by System Account
(GMT) Greenwich Mean Time : Dublin, Edinburgh, Lisbon, London
|
|
|
|
 |
Rating
:
|
 Ratings & Comments
(Click the stars to rate the page) Ratings & Comments
(Click the stars to rate the page)
|
 |
Tags:
|
|
|
|
|