Chapter 3: Investment appraisal – discounted cash flow techniques
Chapter learning objectives
Upon completion of this chapter you will be able to:
- explain the concept of the time value of money
- calculate the future value of a sum by compounding
- calculate the present value (PV) of a single sum using a formula
- calculate the PV of a single sum using discount tables
- calculate the PV of an annuity using a formula
- calculate the PV of an annuity using annuity tables
- calculate the PV of a perpetuity using a formula
- calculate the PV of advanced annuities and perpetuities
- calculate the PV of delayed annuities and perpetuities
- explain the basic principle behind the concept of a cost of capital
- calculate the net present value (NPV) of an investment and use it to appraise the proposal
- discuss the usefulness of NPV as an investment appraisal method and its superiority over non-discounted cash flows (DCF) methods
- calculate the internal rate of return (IRR) of an investment and use it to appraise the proposal
- discuss the usefulness of IRR as an investment appraisal method and its superiority over non-DCF methods
- discuss the relative merits of NPV and IRR.

1 The time value of money
 Money received today is worth more than the same sum received in the future, i.e. it has a time value.
Money received today is worth more than the same sum received in the future, i.e. it has a time value.
This occurs for three reasons:
- potential for earning interest/cost of finance
- impact of inflation
- effect of risk.
 This is a key concept throughout the F9 syllabus.
This is a key concept throughout the F9 syllabus.
Discounted cash flow (DCF) techniques take account of this time value of money when appraising investments.

 The time value of money
The time value of money
Potential for earning interest
If a capital investment is to be justified, it needs to earn atleast a minimum amount of profit, so that the return compensates theinvestor for both the amount invested and also for the length of timebefore the profits are made. For example, if a company could invest$80,000 now to earn revenue of $82,000 in one week's time, a profit of$2,000 in seven days would be a very good return. However, if it takesfour years to earn the money, the return would be very low.
Therefore money has a time value. It can be invested to earninterest or profits, so it is better to have $1 now than in one year'stime. This is because $1 now can be invested for the next year to earn areturn, whereas $1 in one year's time cannot. Another way of looking atthe time value of money is to say that $1 in six years' time is worthless than $1 now.
Impact of inflation
In most countries, in most years prices rise as a result ofinflation. Therefore funds received today will buy more than the sameamount a year later, as prices will have risen in the meantime. Thefunds are subject to a loss of purchasing power over time.
Risk
The earlier cash flows are due to be received, the more certainthey are – there is less chance that events will prevent payment.Earlier cash flows are therefore considered to be more valuable.

2 Compounding
A sum invested today will earn interest. Compounding calculates thefuture or terminal value of a given sum invested today for a number ofyears.
To compound a sum, the figure is increased by the amount of interest it would earn over the period.

 Illustration 1 – Compounding
Illustration 1 – Compounding
An investment of $100 is to be made today. What is the value of the investment after two years if the interest rate is 10%?
Solution

The $100 will be worth $121 in two years at an interest rate of 10%.
This is a fairly straightforward calculation. However, if thequestion asked for the value of the investment after 20 years, it wouldtake a lot longer.

So, to speed up the process, we can use a formula to calculate the future value of a sum invested now. The formula is:
F = P(1 + r)n
where F = Future value after n periods
P = Present or Initial value
r = Rate of interest per period
n = Number of periods
 The terminal value is the value, in n years' time, of a sum invested now, at an interest rate of r%.
The terminal value is the value, in n years' time, of a sum invested now, at an interest rate of r%.

 Test your understanding 1 – Compounding
Test your understanding 1 – Compounding
You have $5,000 to invest now for six years at an interest rate of 5% pa.
What will be the value of the investment after six years?

3 Discounting
In a potential investment project, cash flows will arise at manydifferent points in time. To make a useful comparison of the differentflows, they must all be converted to a common point in time, usually thepresent day, i.e. the cash flows are discounted.
Discounting a single sum
 The present value (PV) is the cash equivalent now of money receivable/payable at some future date.
The present value (PV) is the cash equivalent now of money receivable/payable at some future date.
The PV of a future sum can be calculated using the formula:

This is just a re-arrangement of the formula we used for compounding.
(1 + r)–n is called the discount factor (DF).

 Test your understanding 2 – Discounting a single sum
Test your understanding 2 – Discounting a single sum
What is the PV of $115,000 receivable in nine years' time if r = 6%?

4 The cost of capital
 In the above discussions we referred to the rate of interest. There area number of alternative terms used to refer to the rate a firm shoulduse to take account of the time value of money:
In the above discussions we referred to the rate of interest. There area number of alternative terms used to refer to the rate a firm shoulduse to take account of the time value of money:
- cost of capital
- discount rate
- required return.
 Whateverterm is used, the rate of interest used for discounting reflects thecost of the finance that will be tied up in the investment.
Whateverterm is used, the rate of interest used for discounting reflects thecost of the finance that will be tied up in the investment.
5 The Net Present Value (NPV)
To appraise the overall impact of a project using DCF techniquesinvolves discounting all the relevant cash flows associated with theproject back to their PV.
 If we treat outflows of the project as negative and inflows aspositive, the NPV of the project is the sum of the PVs of all flows thatarise as a result of doing the project.
If we treat outflows of the project as negative and inflows aspositive, the NPV of the project is the sum of the PVs of all flows thatarise as a result of doing the project.
 The NPV represents the surplus funds (after funding the investment) earned on the project, therefore:
The NPV represents the surplus funds (after funding the investment) earned on the project, therefore:
- if the NPV is positive – the project is financially viable
- if the NPV is zero – the project breaks even
- if the NPV is negative – the project is not financially viable
- if the company has two or more mutually exclusive projects under consideration it should choose the one with the highest NPV
- the NPV gives the impact of the project on shareholder wealth.

 What does the NPV actually mean?
What does the NPV actually mean?
Suppose, in an investment problem, we calculate the NPV of certaincash flows at 12% to be – $97, and at 10% to be zero, and yet at 8%the NPV of the same cash flows is + $108. Another way of expressing thisis as follows.
- If the funds were borrowed at 12% the investor would be $97 out of pocket – i.e. the investment earns a yield below the cost of capital.
- If funds were borrowed at 10% the investor would break even – i.e. the investment yields a return equal to the cost of capital.
- If funds were borrowed at 8% the investor would be $108 in pocket – i.e. the investment earns a return in excess of the cost of capital.
In other words, a positive NPV is an indication of the surplusfunds available to the investor now as a result of accepting theproject.

Assumptions used in discounting
Unless the examiner tells you otherwise, the following assumptionsare made about cash flows when calculating the net present value:
- all cash flows occur at the start or end of a year
- initial investments occur T0
- other cash flows start one year after that (T1).
Also note, you should never include interest payments within an NPVcalculation as these are taken account of by the cost of capital.

 Assumptions used in discounting
Assumptions used in discounting
- All cash flows occur at the start or end of a year.
Although in practice many cash flows accrue throughout the year,for discounting purposes they are all treated as occurring at the startor end of a year. Note also that if today(T0) is 01/01/20X0,the dates 31/12/20X1 and 01/01/20X2, although technically separate days,can be treated for discounting as occurring at the same point in time,i.e. at T1.
- Initial investments occur at once (T0), other cash flows start in one year's time (T1).
In project appraisal, the investment needs to be made before thecash flows can accrue. Therefore, unless the examiner specifiesotherwise, it is assumed that investments occur in advance. The firstcash flows associated with running the project are therefore assumed tooccur one year after the project begins, i.e. at T1.


 Test your understanding 3 – Net present value
Test your understanding 3 – Net present value
The cash flows for a project have been estimated as follows:

The cost of capital is 6%.
Convert these cash flows to a PV.
Calculate the net present value (NPV) of the project to assess whether it should be undertaken.


 Test your understanding 4 – Net present value
Test your understanding 4 – Net present value
An organisation is considering a capital investment in new equipment. The estimated cash flows are as follows.

The company's cost of capital is 9%.
Calculate the NPV of the project to assess whether it should be undertaken.

6 Advantages and disadvantages of using NPV
Advantages
 Theoretically the NPV method of investment appraisal is superior to all others. This is because it:
Theoretically the NPV method of investment appraisal is superior to all others. This is because it:
- considers the time value of money
- is an absolute measure of return
- is based on cash flows not profits
- considers the whole life of the project
- should lead to maximisation of shareholder wealth.
Disadvantages
- It is difficult to explain to managers
- It requires knowledge of the cost of capital
- It is relatively complex.

 Advantages and disadvantages of NPV
Advantages and disadvantages of NPV
When appraising projects or investments, NPV is considered to be superior (in theory) to most other methods. This is because it:
- considers the time value of money – discounting cash flows to PV takes account of the impact of interest, inflation and risk over time. (See later sessions for more on inflation and risk.) These significant issues are ignored by the basic methods of payback and annual rate of return (ARR)
- is an absolute measure of return – the NPV of an investment represents the actual surplus raised by the project. This allows a business to plan more effectively
- is based on cash flows not profits – the subjectivity of profits makes them less reliable than cash flows and therefore less appropriate for decision making. Neither ARR nor payback is an absolute measure
- considers the whole life of the project – methods such as payback only consider the earlier cash flows associated with the project. NPV takes account of all relevant flows associated with the project. Discounting the flows takes account of the fact that later flows are less reliable which ARR ignores
- should lead to maximisation of shareholder wealth. If the cost of capital reflects the investors' (i.e. shareholders') required return, then the NPV reflects the theoretical increase in their wealth (see session 18 later). For a company, this is considered to be the primary objective of the business.
However, there are some potential drawbacks:
- It is difficult to explain to managers. To understand the meaning of the NPV calculated requires an understanding of discounting. The method is not as intuitive as techniques such as payback.
- It requires knowledge of the cost of capital. As we will see later (session 18), the calculation of the cost of capital is, in practice, more complex than identifying interest rates. It involves gathering data and making a number of calculations based on that data and some estimates. The process may be deemed too protracted for the appraisal to be carried out.
- It is relatively complex. For the reasons explained above, NPV may be rejected in favour of simpler techniques.

7 Time-saving in the exam
Although you will be able to perform almost any NPV calculationusing the above information, there are a number of time-savingtechniques that can help you in the exam.
Discounting annuities
 An annuity is a constant annual cash flow for a number of years.
An annuity is a constant annual cash flow for a number of years.

 Illustration 2 – Discounting annuities
Illustration 2 – Discounting annuities
A payment of $1,000 is to be made every year for 3 years, the firstpayment occurring in one year's time. The interest rate is 10%. What isthe PV of the annuity?
Solution
The PV of an annuity could be found by adding the PVs of each payment separately.

However, you can see from the table that the sum of all the DF is 2.486.
Therefore the PV can be found more quickly:
$1,000 × 2.486= $2,486.

 The annuity factor (AF) is the name given to the sum of the individual DF.
The annuity factor (AF) is the name given to the sum of the individual DF.
The PV of an annuity can therefore be quickly found using the formula:
PV = Annual cash flow × AF
Like with calculating a discount factor, the AF can be found using a formula.
The formula is:
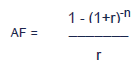

 Test your understanding 5 – Discounting annuities I
Test your understanding 5 – Discounting annuities I
A payment of $3,600 is to be made every year for seven years, thefirst payment occurring in one year's time. The interest rate is 8%.What is the PV of the annuity.

Discounting perpetuities
 A perpetuity is an annual cash flow that occurs forever.
A perpetuity is an annual cash flow that occurs forever.
 It is often described by examiners as a cash flow continuing 'for the foreseeable future'.
It is often described by examiners as a cash flow continuing 'for the foreseeable future'.
The PV of a perpetuity is found using the formula


 Test your understanding 6 – Discounting perpetuities I
Test your understanding 6 – Discounting perpetuities I
What is the present value of $3,000 received in one year's time and for ever if the interest rate is 10%?

Present Value Tables
(1 + r)–n is called the discount factor (DF). In theexam you will be provided with a Present Value table that gives thediscount factors for various different discount rates over various timeperiod. So, to find the DF, for example if r = 10% and n = 5, you can:

 Test your understanding 7 – Discounting a single sum using
Test your understanding 7 – Discounting a single sum using
What amount should be invested now to receive $10,000 in four years' time if r = 8% pa.
Show your workings using the formula approach and then compare this with using the present value table.

Annuity Tables
Just as you are provided with a Present Value Table in the examshowing pre-calculated discount factors, you will also be provided withan Annuity Table (sometimes referred to as a Cumulative Present ValueTable), which provides pre-calculated annuity factors for variousdifferent discount rates over various periods.
So again, you have a choice. For example, for a three-year annuity at 10%:
Note: there might be a small difference due to roundings.
The tables should not be used as a substitute for knowing how touse the formula. Remember, the tables only cover a small range ofdiscount rates and time periods and you may be required to calculate adiscount factor or annuity factor for variables outside of this range.

 Test your understanding 8 – Discounting annuities using tables
Test your understanding 8 – Discounting annuities using tables
A payment of $11,400 is to be made every year for 13 years, thefirst payment occurring in one year's time. The interest rate is 5%.What is the PV of the annuity.
Show you workings using both the formula approach and the annuity table.

Advanced and delayed annuities and perpetuities
The use of annuity factors and perpetuity factors both assume thatthe first cash flow will be occurring in one year's time. Annuity orperpetuity factors will therefore discount the cash flows back to givethe value one year before the first cash flow arose. For standardannuities and perpetuities this gives the present (T0) value since the first cash flow started at T1.
Be careful: if this is not the case, you will need to adjust your calculation.
Advanced annuities and perpetuities
Some regular cash flows may start now (at T0) rather than in one year's time (T1).
Calculate the PV by ignoring the payment at T0 when considering the number of cash flows and then adding one to the annuity or perpetuity factor.

 Advanced annuities: An illustration
Advanced annuities: An illustration
A 5-year $600 annuity is starting today. Interest rates are 10%. Find the PV of the annuity.
Solution
This is essentially a standard 4-year annuity with an additional payment at T0. The PV could be calculated as follows:
PV = 600 + 600 × 3.17 = 600 + 1902 = $2,502
The same answer can be found more quickly by adding 1 to the AF:
PV = 600 × (1 + 3.17) = 600 × 4.17 = $2,502.


 Advanced perpetuities: An illustration
Advanced perpetuities: An illustration
A perpetuity of $2,000 is due to commence immediately. The interest rate is 9%. What is the PV?
Solution
This is essentially a standard perpetuity with an additional payment at T0. The PV could be calculated as follows:


Again, the same answer can be found more quickly by adding 1 to the perpetuity factor.
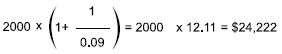


 Additional question - Advanced annuities and perpetuities
Additional question - Advanced annuities and perpetuities
Find the present value of the following cash flows:
(1)A fifteen year annuity of $300 starting at once. Interest rates are 6%.
(2)A seven year annuity of $450 starting immediately. Interest rates are 11%
(3)A perpetuity of $33,000 commencing immediately. Interest rates are 22%
(4)A perpetuity of $14,000 starting at once. Interest rates are 12.5%
The answer to this question can be found after the chapter summary diagram at the end of this chapter.

Delayed annuities and perpetuities
Some regular cash flows may start later than T1.
 These are dealt with by:
These are dealt with by:
(1)applying the appropriate factor to the cash flow as normal
(2)discounting your answer back to T0.

 Delayed annuities: An illustration
Delayed annuities: An illustration
For delayed cash flows, applying the standard annuity factor willfind the value of the cash flows one year before they began, which inthis illustration is T2. To find the PV, an additional calculation is required – the value must be discounted back to T0.
Illustration – Delayed annuities and perpetuities
What is the PV of $200 incurred each year for four years, starting in three year's time, if the discount rate is 5%?
Solution


Care must be taken to discount back the appropriate number ofyears. The figure here was discounted back two years because the firststep gave the value at T2. It can help to draw a timeline asabove and mark on the effect of the first step (as shown with a 1. here)to help you remember.


 Additional question - Delayed annuities and perpetuities
Additional question - Delayed annuities and perpetuities
Find the present value of the following cash flows:
(1)A fifteen year annuity of $300 starting at T3. Interest rates are 6%.
(2)A seven year annuity of $450 starting in five years time. Interest rates are 11%
(3)A perpetuity of $33,000 commencing at T2. Interest rates are 22%
(4)A perpetuity of $14,000 starting in ten years time. Interest rates are 12.5%
The answer to this question can be found after the chapter summary diagram at the end of this chapter.

8 The Internal Rate of Return (IRR)
 The IRR is another project appraisal method using DCF techniques.
The IRR is another project appraisal method using DCF techniques.
The IRR represents the discount rate at which the NPV of aninvestment is zero. As such it represents a breakeven cost of capital.
Decision rule:
- projects should be accepted if their IRR is greater than the cost of capital.

 IRR
IRR
Using the NPV method, PVs are calculated by discounting cash flowsat a given cost of capital, and the difference between the PV of costsand the PV of benefits is the NPV. In contrast, the IRR method of DCFanalysis is to calculate the exact DCF rate of return that the projectis expected to achieve.
If an investment has a positive NPV, it means it is earning morethan the cost of capital. If the NPV is negative, it is earning lessthan the cost of capital. This means that if the NPV is zero, it will beearning exactly the cost of capital.
Conversely, the percentage return on the investment must be therate of discount or cost of capital at which the NPV equals zero. Thisrate of return is called the IRR, or the DCF yield and if it is higherthan the target rate of return then the project is financially worthundertaking.

Calculating the IRR using linear interpolation
The steps in linear interpolation are:
(1)Calculate two NPVs for the project at two different costs of capital
(2)Use the following formula to find the IRR:

where:
L = Lower rate of interest
H = Higher rate of interest
NL = NPV at lower rate of interest
NH = NPV at higher rate of interest.
The diagram below shows the IRR as estimated by the formula.

 Calculating the IRR
Calculating the IRR
The IRR may be calculated by a linear interpolation, i.e. byassuming a linear relationship between the NPV and the discount rate.Plotting a graph would give an approximate IRR, but the same point canalso be found using a formula.

To calculate the exact IRR requires a more complex technique, bestcarried out using an Excel spreadsheet. This will not be expected in theexam.


 Test your understanding 9 – IRR
Test your understanding 9 – IRR
A potential project's predicted cash flows give a NPVof $50,000 at a discount rate of 10% and –$10,000 at a rate of 15%.
Calculate the IRR.

 For the examination the choice of rates to estimate the IRR is lessimportant than your ability to perform the calculation to estimate it.
For the examination the choice of rates to estimate the IRR is lessimportant than your ability to perform the calculation to estimate it.

 Test your understanding 10 – IRR
Test your understanding 10 – IRR
A business undertakes high-risk investments and requires a minimumexpected rate of return of 17% pa on its investments. A proposed capitalinvestment has the following expected cash flows:

(1)Calculate the NPV of the project if the cost of capital is 15%.
(2)Calculate the NPV of the project if the cost of capital is 20%.
(3)Use the NPVs you have calculated to estimate the IRR of the project.
(4)Recommend, on financial grounds alone, whether this project should go ahead.


 Calculating the IRR with even cash flows
Calculating the IRR with even cash flows
There is a simpler technique available, using annuity tables, if the project cash flows are annuities.
(1)Find the cumulative DF, Initial investment ÷ Annual inflow
(2)Find the life of the project, n.
(3)Look along the n year row of the cumulative DF until the closest value is found.
(4)The column in which this figure is found is the IRR.
Illustration – Calculating IRR of a project with even cash flows
Find the IRR of a project with an initial investment of $1.5million and three years of inflows of $700,000 starting in one year.
Solution

- The aim is to find the discount rate (c) that produces an NPV of nil.
- Therefore the PV of inflows (a) must equal the PV of outflows, $1,500,000.
- If the PV of inflows (a) is to be $1,500,000 and the size of each inflow is $700,000, the DF required (b) must be 1,500,000 ÷ 700,000 = 2.143.
- The discount rate (c) for which this is the 3-year factor can be found by looking along the 3-year row of the cumulative DFS shown in the annuity table.
- The figure of 2.140 appears under the 19% column suggesting an IRR of 19% is the closest.


 Calculating the IRR with perpetuities
Calculating the IRR with perpetuities

Illustration – Calculating IRR where cash flows are perpetuities
Find the IRR of an investment that costs $20,000 and generates $1,600 for an indefinitely long period.
Solution
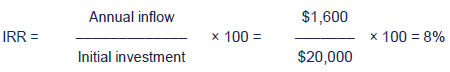


 Test your understanding 11 – IRR with even cash flows
Test your understanding 11 – IRR with even cash flows
Find the IRR of an investment of $50,000 if the inflows are:
(a)$5,000 in perpetuity
(b)$8,060 for eight years.

9 Advantages and disadvantages of IRR
Advantages
The IRR has a number of benefits, e.g. it:
- considers the time value of money
- is a percentage and therefore easily understood
- uses cash flows not profits
- considers the whole life of the project
- means a firm selecting projects where the IRR exceeds the cost of capital should increase shareholders' wealth.
Disadvantages
- It is not a measure of absolute profitability.
- Interpolation only provides an estimate and an accurate estimate requires the use of a spreadsheet programme.
- It is fairly complicated to calculate.
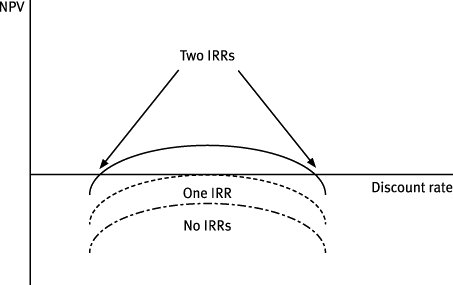
- Non-conventional cash flows may give rise to multiple IRRs which means the interpolation method can't be used.

 Advantages and disadvantages of IRR
Advantages and disadvantages of IRR
Advantages:
- IRR considers the time value of money. The current value earned from an investment project is therefore more accurately measured. As discussed above this is a significant improvement over the basic methods.
- IRR is a percentage and therefore easily understood. Although managers may not completely understand the detail of the IRR, the concept of a return earned is familiar and the IRR can be simply compared with the required return of the organisation.
- IRR uses cash flows not profits. These are less subjective as discussed above.
- IRR considers the whole life of the project rather than ignoring later flows (which would occur with payback for example).
- IRR a firm selecting projects where the IRR exceeds the cost of capital should increase shareholders' wealth. This holds true provided the project cash flows follow the standard pattern of an outflow followed by a series of inflows, as in the investment examples above.
However there are a number of difficulties with the IRR approach:
- It is not a measure of absolute profitability. A project of $1,000 invested now and paying back $1,100 in a year's time has an IRR of 10%. If a company's required return is 6%, then the project is viable according to the IRR rule but most businesses would consider the absolute return too small to be worth the investment.
- Interpolation only provides an estimate (and an accurate estimate requires the use of a spreadsheet programme). The cost of capital calculation itself is also only an estimate and if the margin between required return and the IRR is small, this lack of accuracy could actually mean the wrong decision is taken.
- For example if the cost of capital is found to be 8% (but is actually 8.7%) and the project IRR is calculated as 9.2% (but is actually 8.5%) the project would be wrongly accepted. Note that where such a small margin exists, the project's success would be considered to be sensitive to the discount rate (see session 12 on risk).
- Non-conventional cash flows may give rise to no IRR or multiple IRRs. For example a project with an outflow at T0 and T2 but income at T1 could, depending on the size of the cash flows, have a number of different profiles on a graph (see below). Even where the project does have one IRR, it can be seen from the graph that the decision rule would lead to the wrong result as the project does not earn a positive NPV at any cost of capital.

10 NPV versus IRR
Both NPV and IRR are investment appraisal techniques which discountcash flows and are superior to the basic techniques discussed in theprevious session. However only NPV can be used to distinguish betweentwo mutually-exclusive projects, as the diagram below demonstrates:
The profile of project A is such that it has a lower IRR andapplying the IRR rule would prefer project B. However in absolute terms,A has the higher NPV at the company's cost of capital and shouldtherefore be preferred.
NPV is therefore the better technique for choosing between projects.
 Theadvantage of NPV is that it tells us the absolute increase inshareholder wealth as a result of accepting the project, at the currentcost of capital. The IRR simply tells us how far the cost of capitalcould increase before the project would not be worth accepting.
Theadvantage of NPV is that it tells us the absolute increase inshareholder wealth as a result of accepting the project, at the currentcost of capital. The IRR simply tells us how far the cost of capitalcould increase before the project would not be worth accepting.

 Test your understanding 12 - Appraisal techniques
Test your understanding 12 - Appraisal techniques
Pepper Co is contemplating three available investment opportunities, the cash flows of which are given below.

In each case the initial investment represents the purchase ofplant and equipment whose realisable value will be 20% of initial cost,receivable in addition to the above flow at the end of the life of theproject.
Requirement
For each of the three projects:
(a)Calculate the accounting rate of return (based on the average investment method)
(b)Calculate the payback period
(c)Calculate the net present value using a discount rate of 10%
(d)Calculate the internal rate of return

Chapter summary

 Answer to additional question - Advanced annuities and perpetuities
Answer to additional question - Advanced annuities and perpetuities
(1)This is a standard 14-year annuity with one additional payment at T0.
Step 1: Look up the 14-year AF : AF = 9.295
Step 2: Add 1 : 9.295 + 1 = 10.295
Step 3: Calculate the PV : 300 × 10.295 = $3,088.50
(2)This is a standard 6-year annuity with one additional payment at T0.
Step 1: Look up the 6-year AF : AF = 4.231
Step 2: Add 1 : 4.231 + 1 = 5.231
Step 3: Calculate the PV : 450 × 5.231 = $2,353.95
(3)This is simply a standard perpetuity with one additional payment at T0.
Step 1: Calculate the perpetuity factor : 1/0.22 = 4.545
Step 2: Add 1 : 4.545 + 1 = 5.545
Step 3: Calculate the PV : 33,000 × 5.545 = $182,982
(4)This is simply a standard perpetuity with one additional payment at T0.
Step 1: Calculate the perpetuity factor : 1/0.125 = 8
Step 2: Add 1 : 8 + 1 = 9
Step 3: Calculate the PV : 14,000 × 9 = $126,000


 Answer to additional question - Delayed annuities and perpetuities
Answer to additional question - Delayed annuities and perpetuities
(1)A fifteen year annuity of $300 starting at T3.
Step 1: Look up the 15-year AF : AF = 9.712
Step 2: Discount the annuity as usual : 300 × 9.712 = $2,913.60
Note that this gives the value of the annuity at T2
Step 3: Discount the answer back to T0 : $2,913.60 × 0.890 = $2,593.10
(2)A seven year annuity of $450 starting in five years time.
Step 1: Look up the 7-year AF : AF = 4.712
Step 2: Discount the annuity as usual : 450 × 4.712 = $2,120.40
Note that this gives the value of the annuity at T4
Step 3: Discount the answer back to T0 : 2,120.40 × 0.659 = $1,397.34
(3)A perpetuity of $33,000 commencing at T2.
Step 1: Calculate the perpetuity factor : 1/0.22 = 4.545
Step 2: Discount the perpetuity as usual : 33,000 × 4.545 = $149,985
Note that this gives the value of the perpetuity at T1
Step 3: Calculate the PV : 149,985 × (1 / 1.22) = $122,939
(4)A perpetuity of $14,000 starting in ten years time.
Step 1: Calculate the perpetuity factor : 1/0.125 = 8
Step 2: Discount the perpetuity as usual : 14,000 × 8 = $112,000
Note that this gives the value of the perpetuity at T9
Step 3: Calculate the PV : 112,000 × (1 / 1.1259) = $38,801

Test your understanding answers

 Test your understanding 1 – Compounding
Test your understanding 1 – Compounding
F = $5,000 (1 + 0.05)6
= $5,000 × 1.3401
= $6,700


 Test your understanding 2 – Discounting a single sum
Test your understanding 2 – Discounting a single sum
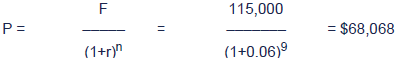


 Test your understanding 3 – Net present value
Test your understanding 3 – Net present value
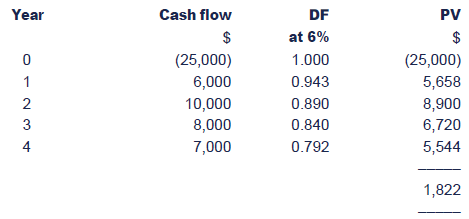
The NPV of the project is positive at $1,822. The project should therefore be accepted.


 Test your understanding 4 – Net present value
Test your understanding 4 – Net present value
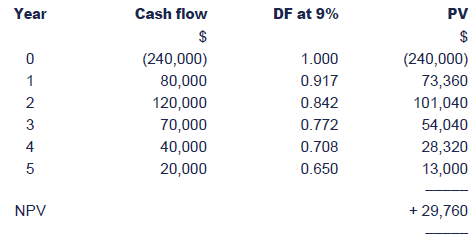
The PV of cash inflows exceeds the PV of cash outflows by $29,760,which means that the project will earn a DCF return in excess of 9%,i.e. it will earn a surplus of $29,760 after paying the cost offinancing. It should therefore be undertaken.


 Test your understanding 5 – Discounting annuities I
Test your understanding 5 – Discounting annuities I
Using the formula:
$3,600 × 5.206 = $18,741.60


 Test your understanding 6 – Discounting perpetuities I
Test your understanding 6 – Discounting perpetuities I



 Test your understanding 7 – Discounting a single sum using
Test your understanding 7 – Discounting a single sum using
The amount to be invested is the PV of the future sum.
P = $10,000/(1.08)4 = $7,350
P = $10,000 × 0.735 = $7,350 (using tables).


 Test your understanding 8 – Discounting annuities using tables
Test your understanding 8 – Discounting annuities using tables
Using the formula:
$11,400 × 9.394= $107,091.60
From the annuity factor tables, the AF = 9.394.


 Test your understanding 9 – IRR
Test your understanding 9 – IRR
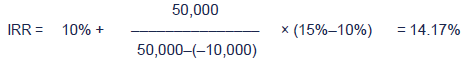


 Test your understanding 10 – IRR
Test your understanding 10 – IRR

The IRR is above 15% but below 20%.
Using the interpolation method:



 Test your understanding 11 – IRR with even cash flows
Test your understanding 11 – IRR with even cash flows

- The aim is to find the discount rate (c) that produces an NPV of nil.
- Therefore the PV of inflows (a) must equal the PV of outflows, $50,000.
- If the PV of inflows (a) is to be $50,000 and the size of each inflow is $8,060, the DF required must be 50,000 ÷ 8,060 = 6.20.
- The discount rate (c) for which this is the 8-year factor can be found by looking along the 8-year row of the cumulative DFS shown in the annuity table.
- The figure of $6.210 appears under the 6% column suggesting an IRR of 6% is the closest.


 Test your understanding 12 – Appraisal techniques
Test your understanding 12 – Appraisal techniques
a. Accounting rate of return
For each project the ARR has been calculated as:

and depreciation has been calculated as initial investment - scrap value.
Project E
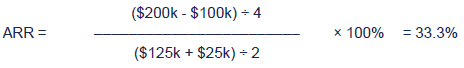
Project F

Project G
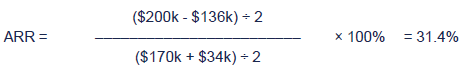
b. Payback
Project E
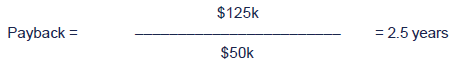
Project F
$120k - (4 × $15k) = $60k
$60k ÷ $200k = 0.3
Payback therefore happens after 4.3 years or approx 4 years, 4 months
Project G
$170k - $120k = $50k
$50k ÷ $80k = 0.63
Payback therefore happens after 1.63 years, or approx 1 years and 7½ months
c. NPV @ 10%
Project E
NPV = ($125k) + $50k × 3.170 + $25k × 0.683 = $50.6k
Project F
NPV = ($120k) + $15k × 3.170 + $200k × 0.621 + $24k × 0.621 = $66.7k
Project G
NPV = ($170k) + $120k × 0.909 + $80k × 0.826 + $34k × 0.826 = $33.2k
d. Internal rate of return
NPV @ 20%
Project E
NPV = ($125k) + $50k × 2.589+ $25k × 0.482 = $16.5k
Project F
NPV = ($120k) + $15k × 2.589 + $200k × 0.402 + $24k × 0.402 = $8.9k
Project G
NPV = ($170k) + $120k × 0.833 + $80k × 0.694 + $34k × 0.694 = $9.1k
IRRs =
Project E

Project F
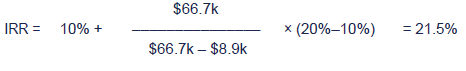
Project G


|
Created at 5/24/2012 4:10 PM by System Account
(GMT) Greenwich Mean Time : Dublin, Edinburgh, Lisbon, London
|
Last modified at 5/25/2012 12:54 PM by System Account
(GMT) Greenwich Mean Time : Dublin, Edinburgh, Lisbon, London
|
|
|
|
 |
Rating
:
|
 Ratings & Comments
(Click the stars to rate the page) Ratings & Comments
(Click the stars to rate the page)
|
 |
Tags:
|
|
|
|
|