Chapter 3: Planning with limiting factors

Chapter learning objectives

Upon completion of this chapter you will be able to:

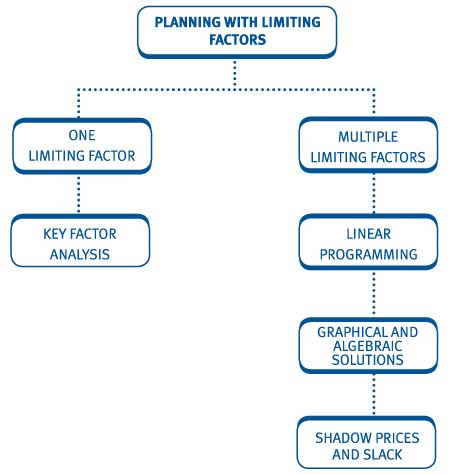
• select an appropriate technique, where there is one limiting factor/key factor, to achieve desired organisational goals.
• determine the optimal production plan where an organisation is restricted by a single limiting factor, including within the context of 'make' or 'buy' decisions (covered separately in Chapter 5).
• select an appropriate technique, where there are several limiting factors/key factors, to achieve desired organisational goals.
• formulate a linear programming problem involving two products.
• determine the optimal solution to a linear programming problem using a graphical approach.
• use simultaneous equations to determine where the two lines cross to solve a multiple scarce resource problem.
• explain shadow prices (dual prices) and discuss their implications on decision making and performance management in multiple limited resource situations.
• calculate shadow prices (dual prices) and discuss their specific implications on decision making and performance management.
• explain the implications of the existence of slack, in multiple limited resource situations, for decision making and performance management.
• calculate slack and explain the specific implications of the existence of the slack for decision making and performance management.

1 Introduction

Limiting factor analysis was covered in F2. In F5 the maindifference is that the examination contains written questions so issuescan be examined in more depth with scope for discussion. With linearprogramming the F5 syllabus also includes new aspects not seen before inF2.

Limiting factors

Firms face many constraints on their activity and plan accordingly:

• limited demand ;
• limited skilled labour and other production resources ;
• limited finance (‘capital rationing').

Examination questions will focus on the problem of scarce resources that prevent the normal plan being achieved.

For example, a firm is facing a labour shortage this month due tosickness and, as a result, cannot produce the number of units that itwould like to. How should its production plan be revised?

2 Planning with one limiting factor

Key factor analysis – calculations

The usual objective in questions is to maximise profit. Given thatfixed costs are unaffected by the production decision in the short run,the approach should be to maximise the contribution earned.

If there is one limiting factor, then the problem is best solved using key factor analysis.

Step 1: identify the scarce resource.

Step 2: calculate the contribution per unit for each product.

Step 3: calculate the contribution per unit of the scarce resource for each product.

Step 4: rank the products in order of the contribution per unit of the scarce resource.

Step 5: allocate resources using this ranking and answer the question.

Test your understanding 1

X Ltd makes three products, A, B and C, of which unit costs, machine hours and selling prices are as follows:

Sales demand for the period is limited as follows.

Company policy is to produce a minimum of 1,000 units of Product A.

The supply of materials in the period is unlimited, but machine hours are limited to 200,000 and direct labour hours to 5,000.

Required:

Indicate the production levels that should be adopted for the threeproducts in order to maximise profitability, and state the maximumcontribution.

3 Several limiting factors – linear programming

When there is only one scarce resource the method above (key factoranalysis) can be used to solve the problem. However where there are twoor more resources in short supply which limit the organisation'sactivities then linear programming is required to find the solution.

In examination questions linear programming is used to:

• maximise contribution and/or
• minimise costs.

Formulating a linear programming problem involving two variables

The steps involved in linear programming are as follows:

Note: Linear programming calculations will only involve two variables in exam questions.

Illustration 1 - Linear programming

A company produces two products in three departments. Details areshown below regarding the time per unit required in each department, theavailable hours in each department and the contribution per unit ofeach product: 

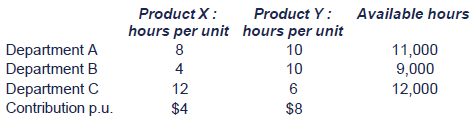
Required

Determine, using a step-by-step approach, what the optimum production plan is.

Linear Programming - Solution

To determine what the optimum production plan is, we will follow the linear programming steps :

Step 1 : Define the variables

Let 'x' be the number of units of X to produce; Let 'y' be the number of units of Y to produce.

Step 2 : Define and formulate the objective function

Objective function: to maximise contribution C= $4x + $8y

Step 3 : Formulate the constraints

Subject to:
In Department A, 8x + 10y ≤ 11,000 hours
In Department B, 4x + 10y ≤  9,000 hours
In Department C, 12x +  6y ≤ 12,000
0≤x,y

Step 4 : Draw a graph identifying the feasible region 

To draw Constraint 1 (constraint in Department A), we take theinequality '8x + 10y ≤ 11,000 hours' and turn it into an equation : 8x+ 10y = 11,000.

To draw this constraint, we need two points. If X = 0, Y = 11,000÷ 10 so Y = 1,100. Likewise, if Y = 0, X = 11,000 ÷ 8 so X = 1,375.

To draw Constraint 2 (Department B) : If X = 0, Y = 900 and if Y = 0, X = 2,250.

To draw Constraint 3 (Department C) : If X = 0 , Y = 2,000 and if Y = 0, X = 1,000

Step 5 : Finding the optimum solution - Using the isocontribution line

We do not know the maximum value of the objective function;however, we can draw an isocontribution (or 'profit') line that showsall the combinations of x and y that provide the same total value forthe objective function.

If, for example, we need to maximise contribution $4x + $8y, we candraw a line on a graph that shows combination of values for x and ythat give the same total contribution, when x has a contribution of $4and y has a contribution of $8.

Any total contribution figure can be picked, but a multiple of $4 and $8 is easiest.

• For example, assume 4x + 8y = 4,000. This contribution line could be found by joining the points on the graph x = 0, y = 500 and x = 1,000 and y = 0.
• Instead, we might select a total contribution value of 4x + 8y = $8,000.This contribution line could be found by joining the points on the graph x = 0, y = 1,000 and x = 2,000 and y = 0.
• When drawing both of these contribution lines on a graph, we find that the two lines are parallel and the line with the higher total contribution value for values x and y ($8,000) is further away from the origin of the graph (point 0).
• This can be used to identify the solution to a linear programming problem. Draw the isocontribution line showing combinations of values for x and y that give the same total value for the objective function.
• Look at the slope of the contribution line and, using a ruler, identify which combination of values of x and y within the feasible area for the constraints is furthest away from the origin of the graph. This is the combination of values for x and y where an isocontribution line can be drawn as far to the right as possible that just touches one corner of the feasible area. This is the combination of values of x and y that provides the solution to the linear programming problem.

Optimum corner is Corner C, the intersection of:

The optimum production plan is to produce 500 units of Product X and700 units of Product Y; The contribution at this point is maximised C =(500 x $4) + (700 x $8) = $7,600.

Test your understanding 2 - Steps 1 to 3

Hebrus Inc manufactures summerhouses and garden sheds. Each productpasses through a cutting process and an assembly process. Onesummerhouse, which makes a contribution of $50, takes six hours' cuttingtime and four hours' assembly time; while one shed makes a contributionof $40, and takes three hours' cutting time and eight hours' assemblytime. There is a maximum of 36 cutting hours available each week and 48assembly hours.

Cutters are paid $10 per hour and assembly workers $15 per hour.

Required:

Formulate the linear programming problem.

Step 4: Drawing the graph and identifying the feasible region

Drawing the graph

• Step 4 of the linear programming model is to represent the constraints as straight lines on a graph.
• In order to plot the constraints it is normally best to compute the intercepts of the equalities on the horizontal and vertical axes. Thus, x and y are each set equal to zero in turn and the value of y and x computed in these circumstances.

Revision of graphing a straight line

Step 4 of the linear programming model is to represent theconstraints as straight lines on a graph. We do this below. In themeantime, this section contains basic revision for students who are notfamiliar with the process of graphing a straight line.

To begin with, we must have a linear relationship between two measurements.

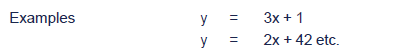
Note:

(1)   To recognise a linear relationship the equation must have only ‘x' not ‘x' to the power of anything, e.g. x².

(2)   A straight line has two characteristics:

Therefore, the gradient is 2 and the point at which the line cuts the y axis is 3.

To draw a straight line graph we only need to know two points that can then be joined.

Consider the following two equations:

In order to draw the graphs of these equations it is necessary todecide on two values for x and then to calculate the correspondingvalues for y. Let us use x = 0 and 3. These calculations are bestdisplayed in tabular form.

So to draw the first line we plot the points (0, 3) and (3, 9) andsimply join them up. Similarly, for the second line we plot the points(0, -2) and (3, 4) and join them up.

Note: The lines are parallel because the equations have the same gradient of 2.

Test your understanding 3 - Step 4

Using the information from the Hebrus example (TYU 2) you arerequired to plot the constraints on a graph and indicate on the graphthe feasible region.

Identifying the feasible region

• Having inserted the straight lines in the graph, we are then ready to work out what is called the feasible region.
• The feasible region shows those combinations of variables which are possible given the resource constraints.
• In the TYU above the original constraints were '≤' types, so the feasible region is shown by the area bounded by the thick black line on the graph. Production can be anywhere in this area.
• The lines drawn on the graph represent equations where the LHS equals the RHS. However, the original constraint was either '≤' or '≥'.
• A '≤' type constraint is represented by all points on the line AND all points in the area below the line (i.e. nearer to the origin - the point x=0,y=0)
• A '≥' type constraint is represented by all points on the line AND all points in the area above the line (i.e. away from the origin).
• Watch out in the examination for constraints that show minimum amounts required as well as maximum amounts of constraints available. Typically in questions these tend to be a government quota that a minimum amount of one of the output needs to be produced.

Step 5: Finding the optimal solution using the graph

Having found the feasible region the problem now is to find the optimal solution within this feasible region.

There are two approaches to this final stage.

• By inspection it is clear that the maximum contribution will lie on one of the corners of the feasible region. The optimal solution can be reached simply by calculating the contributions at each corner. This approach is not recommended in the exam since it tends to be quite time consuming.
• By drawing an iso-contribution line (an objective function for a particular value of C), which is a line where all points represent an equal contribution. This is the recommended approach, particularly for more complex problems.

Test your understanding 4 - Steps 5 and 6

Using the Hebrus example again (TYU 2 and 3) you are required to find the optimal solution using the graph (Step 5).

Calculate the contribution at this point (Step 6).

Solving the problem using simultaneous equations

You may consider that the whole process would be easier by solvingthe constraints as sets of simultaneous equations and not bothering witha graph. This is possible and you may get the right answer, but such atechnique should be used with caution and is not recommended until youhave determined graphically which constraints are effective indetermining the optimal solution.

Furthermore, if the question asks for a graphical solution, then a graph must be used.

The technique can, however, be used as a check, or to establish theexact quantities for the optimal solution when the graph does not givesufficient accuracy.

Test your understanding 5 - Simultaneous equations

Using the Hebrus example again (TYU 2 - 4) you are required to use simultaneous equations to verify the optimal point.

Test your understanding 6 - Additional example

Alfred Co is preparing its production plan for the coming month. Itmanufactures two products, the flak trap and the sap trap. Details areas follows.

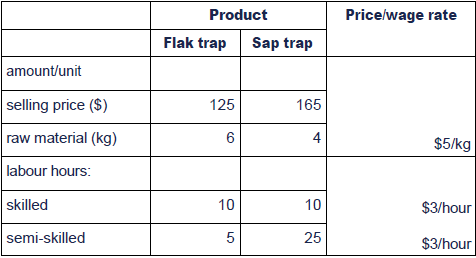
The company's fixed overhead absorption rate (OAR) is $1/labourhour (for both skilled and semi-skilled labour). The supply of skilledlabour is limited to 2,000 hours/month and the supply of semi-skilledlabour is limited to 2,500 hours/month. At the selling prices indicated,maximum demand for flak traps is expected to be 150 units/month and themaximum demand for sap traps is expected to be 80 units/month.

Required:

(a)Formulate the constraints for Alfred Co

(b)Plot the constraints on a graph and indicate on the graph the feasible region.

(c)Using the graph find the optimal production plan.

(d)Use simultaneous equations to accuratelycalculate the quantities produced at the optimal point and calculate themaximum contribution at this point.

Test your understanding 7 - Minimising costs

J Farms Ltd can buy two types of fertiliser which contain the following percentage of chemicals:

For a certain crop the following minimum quantities (kg) are required:

Type X costs £10 per kg and type Y costs £5 per kg. J Farms Ltdcurrently buys 1,000 kg of each type and wishes to minimise itsexpenditure on fertilisers.

(a) Write down the objective function and the constraints for J Farms Ltd.

(b) Draw a graph to illustrate all the constraints (equations/ inequalities), shading the feasible region.

(c) Recommend the quantity of each type of fertiliser which should be bought and the cost of these amounts.

(d) Find the saving J Farms Ltd can make by switching from its current policy to your recommendation.

Limiting factor analysis – discussion aspects

Assumptions

• There is a single quantifiable objective – e.g. maximise contribution. In reality there may be multiple objectives such as maximising return while simultaneously minimising risk.
• Each product always uses the same quantity of the scarce resource per unit. In reality this may not be the case. For example, learning effects may be enjoyed.
• The contribution per unit is constant. In reality this may not be the case:
  • the selling price may have to be lowered to sell more
  • there may be economies of scale, for example a discount for buying in bulk.
• Products are independent – in reality:
  • customers may expect to buy both products together
  • the products may be manufactured jointly together.
• The scenario is short term. This allows us to ignore fixed costs.

The assumptions apply to the analysis used when there is one limiting factor or if there are multiple limiting factors.

Shadow prices and slack

Slack

Slack is the amount by which a resource is under-utilised.It will occur when the optimum point does not fall on a given resourceline.

Slack is important because unused resources can be put to another use, e.g. hired out to another manufacturer.

Illustration 2 - Slack

In the Hebrus example (TYU 2-5), the optimum point Q lies on boththe cutting and assembly time lines. Therefore both resources are fullyutilised and are referred to as critical constraints.

In the Alfred Co example (TYU 6), the optimum point D lies on theintersection of the skilled labour line (10x + 10y = 2,000) and themaximum demand line for flak traps (x = 150). At this point there isunutilised semi-skilled labour. This means that slack exists forsemi-skilled labour. Semi-skilled labour is a non-critical constraintand this unutilised resource should be used elsewhere in the business togenerate contribution.

Shadow (or dual) prices

• The shadow price of a resource can be found by calculating the increase in value (usually extra contribution) which would be created by having available one additional unit of a limiting resource at its original cost.
• It therefore represents the maximum premium that the firm should be willing to pay for one extra unit of each constraint. This aspect is discussed in more detail below.
• Non-critical constraints will have zero shadow prices as slack exists already.

Calculating shadow prices

The simplest way to calculate shadow prices for a critical constraint is as follows:

Step 1: Take the equations of the straight lines thatintersect at the optimal point. Add one unit to the constraintconcerned, while leaving the other critical constraint unchanged.

Step 2: Use simultaneous equations to derive a new optimal solution

Step 3: Calculate the revised optimal contribution. The increase is the shadow price for the constraint under consideration.

Test your understanding 8 - Shadow prices

In Hebrus the optimal solution was determined to be x=4 and y=4giving an optimal contribution of $360. This solution was at theintersection of the lines:

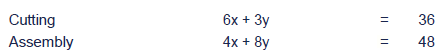
Required:

Suppose one extra hour was available for the cutting process.Calculate the shadow price for this additional hour of cutting time.

Additional example on shadow prices

Using the following data, calculate the shadow price for machining time.

Maximise C = 80x + 75y (contribution), subject to

(i)20x + 25y ≤ 500 (machining time)

(ii) 40x + 25y ≤ 800 (finishing time)

The optimal solution at the intersection of the above constraints is: x = 15, y = 8.

Solution

Step 1: Machining time – the constraints become:

(i)20x + 25y ≤ 501

(ii) 40x + 25y ≤ 800

Step 2: Subtracting (i) from (ii) gives 20x = 299 and thus x = 14.95

Inserting into (i) gives

(20 ×14.95) + 25y = 501

25y                        = 202

y                            = 8.08

Step 3: Original contribution = (15 × $80) + (8 × $75) = $1,800.

Amended contribution = (14.95 × $80) + (8.08 × $75) = $1,802.

The shadow price per machine hour is thus $2.

Implications of shadow prices

• Management can use shadow prices as a measure of the maximum premium that they would be willing to pay for one more unit of the scarce resource.
• However, the shadow price should be considered carefully. For example, the shadow price of labour may be calculated as $20 per hour. However, it may be possible to negotiate a lower shadow price than this.
• In addition, if more of the critical constraint is obtained, the constraint line will move outwards altering the shape of the feasible region. After a certain point there will be little point in buying more of the scarce resource since any non-critical constraints will become critical.

Additional example on linear programming

Suppose a linear programming problem gives the following results.

Required:

(a) Which two constraints give rise to the optimal solution?

(b) Overtime is paid at 'time-and-a-half'. Is it worth paying overtime to help relax constraints?

(c) A new product has been proposed with the following proposed costs and revenues.

Assuming that the constraints cannot be relaxed, should the new product be manufactured?

Solution

(a) Critical constraints have non-zero dualprices, so the optimal solution will be at the intersection of skilledlabour and materials.

(b) For skilled labour overtime will cost $30per hour and the benefit will be 20+12=$32 per hour. The overtime isthus worth while and will generate a net $2 per hour benefit.

(c) The profit statement can be revised using as follows:

Incorporating the contribution lost elsewhere by reallocating scarce resources, the new product is not viable.

4 Chapter summary

Test your understanding answers

Test your understanding 1

Step 1: Identify the scarce resource (this may be done for you in examination questions).

At potential sales level:

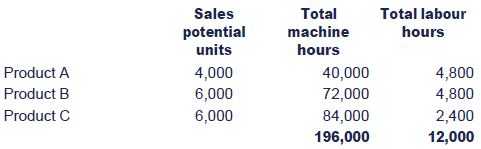
Thus, labour hours are the limiting factor.

Step 2: calculate the contribution per unit for each product.

This has been done for us in the question

Step 3: calculate the contribution per unit of the scarce resource for each product, i.e. per labour hour

Product A $6/ 1.2= $5.00

Product B $5/0.8= $6.25

Product C $4/0.4= $10.00

Step 4: rank the products in order of the contribution per unit of the scarce resource.

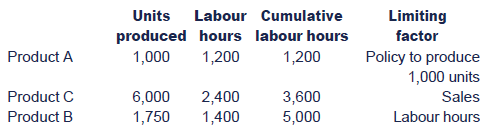
Thus, production should be concentrated first on C, up to the maximum available sales, then B, and finally A.

However, a minimum of 1,000 units of A must be produced.

Step 5: allocate resources using this ranking and answer the question, i.e. state the maximum contribution.

Taking these factors into account, the production schedule becomes:

The maximum contribution is therefore as follows.

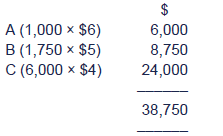
Test your understanding 2 - Steps 1 to 3

Step 1 – define the variables
Let x = the number of summerhouses produced each week

(Note: Be careful to specify the time periods involved.)

Step 2 – define and formulate the objective function.

The objective here is to maximise contribution C, given by: Maximise Contribution = 50x + 40y

Step 3 – formulate the constraints.

The constraints (limitations) here are the amounts of cutting and assembly time available.

If 1 summerhouse requires 6 hours' cutting time,

If 1 shed requires 3 hours' cutting time,

Hence total cutting time required = 6x + 3y hours.

Similarly, if one summerhouse and one shed require 4 and 8 hours'assembly time respectively, the total assembly time for x summerhousesand y sheds will be 4x + 8y.

The conventional way of setting out the constraints is to place the units utilised on the left, and those available on the right; the inequality sign is the link.

In addition, two other logical constraints must be stated, i.e. x > 0 and  y > 0

These simply state that negative amounts of garden sheds or summerhouses cannot be made.

Test your understanding 3 - Step 4

The cutting time constraint is an inequality 6x + 3y ≤ 36 whichrepresents a region on the graph. To identify this region we draw theline 6x + 3y = 36 (equality) and then determine which side of the lineis feasible. This process is repeated for each constraint.

For the equation 6x + 3y = 36 – cutting time constraint

when x = 0, y = 36/3 = 12

when y = 0, x =36/6 = 6

To graph this constraint, we draw a straight line between the points (0, 12) and (6, 0).

For the equation 4x + 8y = 48 – assembly time constraint

when x = 0, y = 48/8 = 6

when y = 0, x =48/4 = 12

To graph this constraint, we draw a straight line between the points (0, 6) and (12, 0).

The constraints can now be represented graphically:

The original constraints were '≤' types, so the feasible region isshown by the area bounded by the thick black line on the graph.Production can be anywhere in this area.

Test your understanding 4 - Steps 5 and 6

Step 5: Finding the optimal solution using the graph.

Let's first consider what we mean by an iso-contribution line.

An iso-contribution line is a line where all the points represent an equal contribution.

The contribution for Hebrus is given by the equation, C = 50x + 40y (from Step 2).

• If we choose a contribution of, say, $200 we can draw an iso-contribution line 200 = 50x + 40y

• If we choose another contribution of, say, $240 we can draw an iso-contribution line 240 = 50x + 40y

when x = 0, y = 240/40 = 6

when y = 0, x = 240/50 = 4.8

To graph the line, we draw a straight line between the points (0, 6) and (4.8, 0). This line is shown on the graph below.

The iso-contribution lines move to and from the origin in parallel;the arrow indicates increasing contribution. The object is to get onthe highest contribution line within (just touching) the bindingconstraints.

The optimum point is found by drawing an example of aniso-contribution line on the diagram (any convenient value of C willdo), and then placing a ruler against it. Then, by moving the ruler awayfrom the origin (in the case of a maximisation problem) or towards theorigin (in the case of a minimisation problem) but keeping it parallelto the iso-contribution line, the last corner of the feasible solutionspace which is met represents the optimum solution.

To find the optimal point for Hebrus we have used aniso-contribution line for a contribution of $165. However, either of theiso-contribution lines discussed above, or another iso-contributionline, could have been used instead.

165 = 50x + 40y

when x = 0, y = 165/40 = 4.125

when y = 0, x = 165/50 = 3.3

To graph the line, we draw a straight line between the points (0, 4.125) and (3.3, 0). This line is shown on the graph below.

Optimal point: The highest available iso-contribution line occurs at point Q.

Step 6: Answer the question, i.e. calculate the contribution at the optimal point.

Reading from the graph, at point Q x = 4 and y = 4. This gives a maximum contribution of C = (50 × 4) + (40 × 4) = $360.

Test your understanding 5 - Simultaneous equations

Step 1: Take the equations of the two constraints that cross at the optimal point.

The optimal point is point Q. This is at the intersection of the two constraint lines:

4x + 8y = 48    this will be called (a)

6x + 3y = 36    this will be called (b)

Step 2: Multiply both equations in order to get the same number of x's or y's in each equation

(a) multiplied by 3 gives      12x + 24y = 144

(b) multiplied by 2 gives       12x + 6y = 72

Step 3: Subtract one equation from the other to eliminate either x or y

(a)                12x + 24y = 144

minus (b)     12x + 6y = 72

gives           0x + 18y = 72

Therefore, y = 72/18 = 4 (this is the same number of garden sheds found using the graph).

Step 4: Use any equation to find the missing value, i.e. either x or y

Using the value y=4 we can find the value of x. Any of the equations above can be used. For example:

4x + 8y = 48

4x + (8 × 4) = 48

4x = 16

x = 16/ 4 = 4 (this is the same number of summerhouses found using the graph.

Step 5: Answer the question

The optimal point is at x=4 and y=4. This gives a maximum contribution of C = (50 × 4) + (40 × 4) = $360 (as per TYU4).

Test your understanding 6 - Additional example

(a) Step 1: define variables

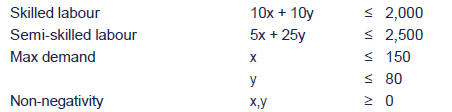
(b) Step 4: draw a graph and identify the feasible region

Skilled labour: x = 0, y = 2,000/10 = 200

y = 0, x = 2,000/10 = 200

We simply join up the points (0, 200) and (200, 0).

Semi-skilled labour: x = 0, y = 2,500/25 = 100

y = 0, x = 2,500/5 = 500

We join up the points (0, 100) and (500, 0)

This gives a feasibility region of 0ABCDE.

(c) Step 5: use the graph to solve the optimal production plan

Objective is to maximise contribution C = 50x + 40y.

The iso-contribution line C=2,000 has been drawn to establish the gradient and identify the optimal solution at point D:

It is difficult to read the precise co-ordinates for point D butit is at the intersection of the two lines x = 150 and 10x + 10y =2,000. This corresponds to 150 units of x (flak traps) and approximately50-60 units of y (sap traps). The exact amounts can be found usingsimultaneous equations (see below).

(d) Use simultaneous equations to accuratelycalculate the quantities produced at the optimal point and calculate themaximum contribution at this point.

Test your understanding 7 - Minimising costs

(a)The chemicals are given in percentage terms that are converted to decimals.

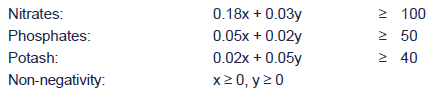
(b) Step 4: draw the graph and identify the feasible region

(c) Step 5: find the optimal solution using the graph

(d) The current policy costs: 1,000 ($10) + 1,000 ($5) = $15,000, so the saving made is of $(15,000 — 10,476) = $4,524.

Test your understanding 8 - Shadow prices

Step 1: Take the equations of the straight lines thatintersect at the optimal point. Add one unit to the constraintconcerned, while leaving the other critical constraint unchanged.

We would then need to solve:

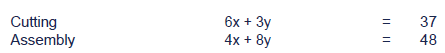
Step 2: Use simultaneous equations to derive a new optimal solution

The simultaneous equations above can be solved in the same way aswas seen in the previous TYU's. This gives and optimum vale of y =3.888… and x = 4.222…

Step 3: Calculate the revised optimal contribution. The increase is the shadow price for the constraint under consideration.

The contribution. C = 50x + 40y.

At the revised optimal point this gives a revised contribution of C = (50 × 4.222…) + (40 × 3.888…) = $366.67 .

The increase of $6.67 ($366.67 - $360) is the shadow price forcutting time per hour. This represents the premium that the firm wouldbe willing to pay for each extra hour of cutting time. The current costis $10 per hour and therefore the maximum price that would be paid foran extra hour of cutting time is $16.67.

Note: A similar calculation can be done for assembly time giving a shadow price of $2.50 per hour.

Rating :	Ratings & Comments  (Click the stars to rate the page)

Tags: