Chapter 3: The weighted average cost of capital (WACC)

Chapter learning Objectives

Upon completion of this chapter you will be able to:

• calculate a cost of equity using Dividend Valuation Model (DVM), the Capital Asset Pricing Model (CAPM) and Modigliani and Miller's Proposition 2 formula.
• calculate a cost of debt using DVM, CAPM and credit spreads.
• understand how lenders set their interest rates on debt finance.
• calculate a weighted average cost of capital.
• understand the circumstances in which the WACC can be used as a project discount rate.

1 The weighted average cost of capital (WACC)

Overview of the WACC

A key consideration in financial management is the firm's WACC. TheWACC is derived by finding a firm's cost of equity and cost of debt andaveraging them according to the market value of each source of finance.The formula for calculating WACC is given on the exam formula sheet as:

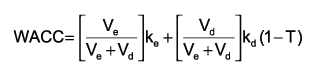
Explanation of terms

V_e and V_d are the market values of equity and debt respectively.

k_e and k_d are the returns required by the equity holders and the debt holders respectively.

T is the corporation tax rate.

k_e is the cost of equity.

k_d(1-T) is the cost of debt.

This chapter reviews the basic techniques for deriving cost ofequity and cost of debt from the F9 paper, and adds some more advancedtechniques too.

2 The cost of equity (ke)

Methods of calculating k_e

The three main methods of calculating k_e are:

• the Capital Asset Pricing Model (CAPM)
• the Dividend Valuation Model (DVM)
• Modigliani and Miller's Proposition 2 formula

The formulae for these methods are all given on the exam formula sheet.

The Capital Asset Pricing Model (CAPM)

The CAPM derives a required return for an investor by relatingreturn to the level of systematic risk faced by an investor - note thatthe CAPM is based on the assumption that all investors are welldiversified, so only systematic risk is relevant.

The CAPM formula is:

Required return ( k_e ) = R_f + ß_i (E(R_m) - R_f)

where:

R_f = risk free rate

E(R_m) = expected return on the market

N.B. (E(R_m) - R_f) is called the equity risk premium

ß_i = beta factor = systematic risk of the firm or project compared to market.

The portfolio effect

The CAPM model is based upon the assumption that investors are welldiversified, so will have eliminated all the unsystematic (specific)risk from their portfolios. The beta factor is a measure of the level ofsystematic risk (general, market risk) faced by a well diversifiedinvestor - see more details on beta factors below.

The risk reduction through diversifying is known as the portfolio effect.

If an investor is not well diversified, the level of risk affectingthe investor can be calculated using the 2 asset portfolio formula:

Overall risk (standard deviation) = (w_a²s_a²+w_b²s _b²+2w_aw_br_abs_as _b)^½

where

w_a and w_b are the proportions invested in two investments a and b

s_a and s_b are the risks associated with investments a and b (standard deviations)

r_ab is the correlation coefficient of the investments a and b

The beta factor

The beta factor indicates the level of systematic risk faced by an investor.

A beta > 1 indicates above average risk, while beta < 1="" means="" relatively="" low="">

Beta factors are derived by statistically analysing returns from aparticular share over a period compared to the overall market returns.If the returns on the individual share are more volatile than theoverall market, the firm's beta will be greater than 1.

Illustration of the use of the CAPM formula

Gillespie Co has a beta factor of 1.73. The current return on arisk free asset is 3% per annum and the equity risk premium is 12%.

Hence, using CAPM, Gillespie Co's cost of equity (return required by the shareholders) is
3% + (1.73 × 12%) = 23.76%.

Which beta factor to use?

To calculate the current cost of equity of a firm, the current beta factor can be used.

However, if the firm's current beta factor cannot be derived easily, a proxy beta may be used.

A proxy beta is usually found by identifying a quoted company with asimilar business risk profile and using its beta. However, whenselecting an appropriate beta from a similar company, account has to betaken of the gearing ratios involved.

The beta values for companies reflect both:

• business risk (resulting from operations)
• finance risk (resulting from their level of gearing).

There are therefore two types of beta:

• “Asset” or “ungeared” beta, ß_a , which reflects purely the systematic risk of the business area.
• “Equity” or “geared” beta, ß_e , which reflects the systematic risk of the business area and the company specific gearing ratio.

In the exam, you will often have to degear the proxy equity beta(using the gearing of the quoted company) and then regear to reflect thegearing position of the company in question.

The formula to regear and degear betas is:

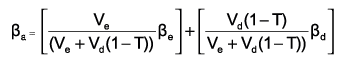
However, ß_d (beta value for debt) is often assumed tobe zero, because of the low risk of being a debt holder, so thisequation often simplifies to give

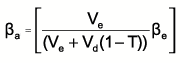
Test your understanding 1

The directors of Moorland Co, a company which has 75% of itsoperations in the retail sector and 25% in manufacturing, are trying toderive the firm's cost of equity. However, since the company is notlisted, it has been difficult to determine an appropriate beta factor.Instead, the following information has been researched:

Retail industry - quoted retailers have an average equity beta of 1.20, and an average gearing ratio of 20:80 (debt:equity).

Manufacturing industry - quoted manufacturers have an average equity beta of 1.45 and an average gearing ratio of 45:55 (debt:equity).

The risk free rate is 3% and the equity risk premium is 6%. Tax oncorporate profits is 30%. Moorland Co has gearing of 50% debt and 50%equity by market values. Assume that the risk on corporate debt isnegligible.

Required:

Calculate the cost of equity of Moorland Co using the CAPM model.

The dividend valuation model (DVM)

Theory: The value of the company/share is the present valueof the expected future dividends discounted at the shareholders’required rate of return.

Assuming a constant growth rate in dividends, g:

P₀ = D₀(1 + g) / (k_e - g)

(this formula is given on the formula sheet)

Explanation of terms

D ₀ = current level of dividend

P ₀ = current share price

g = estimated growth rate

If we need to derive ke the formula can be rearranged to:

ke = [D₀ (1+g) / P₀ ] + g

Illustration of the DVM formula

Cocker Co has just paid a dividend of 14 cents per share. In recentyears, annual dividend growth has been 3% per annum, and the currentshare price is $1.48.

Using the DVM formula, the cost of equity is [0.14 × 1.03 / 1.48] + 0.03 = 12.7%

Deriving g in the DVM formula

There are two ways of estimating the likely growth rate of dividends:

• Extrapolating based on past dividend patterns.
• Assuming growth is dependent on the level of earnings retained in the business.

Estimating dividend growth from past dividend patterns

This method assumes that the past pattern of dividends is a fair indicator of the future.

The formula for extrapolating growth can therefore be written as:

where:

n = number of years of dividend growth

This method can only be used if:

• recent dividend pattern is considered typical
• historical pattern is expected to continue.

As a result, this method will usually only be appropriate to predict growth rates over the short term.

Illustration of the calculation

A company currently pays a dividend of 32¢; five years ago the dividend was 20¢.

Estimate the annual growth rate in dividends.

Solution

Since growth is assumed to be constant, the growth rate, g, can beassumed to have been the same in each of the 5 years, i.e. the 20¢ willhave become 32¢ after 5 years of constant growth.

20¢ × (1 + g)⁵ = 32¢

or (1 + g)⁵ = 32/20 = 1.6

1 + g = 1.6^1/5 ≈ 1.1, so g = 0.1 or 10%.

Estimating growth using the earnings retention model (Gordon’s growth model)

This model is based on the assumption that:

• growth is primarily due to the reinvestment of retained earnings

The formula is therefore:

g = r × b

where:

b = earnings retention rate

r = rate of return to equity

What is r?

At F9 level, r was considered to be the Accounting Rate of Return on equity calculated as:

r = PAT / opening shareholders' funds

However, at P4 we need to re-examine this assumption. The weakness of the ARR as a measure of return is that:

• it ignores the level of investment in intangible assets
• in the long run, the return on new investment tends to the cost of equity.

Hence, if a short term growth rate is required, the ARR provides afair approximation for use in the growth model. However, if a long termgrowth rate is needed, k_e should be used as the percentage return. To avoid a recursion problem, this should be derived using CAPM.

Modigliani and Miller's Proposition 2 formula

Modigliani and Miller's gearing theory is covered in the later chapter on Capital Structure and Financing.

As part of their theory, they derived a formula which can be used to derive a firm's cost of equity:

k_e = k_eⁱ + (1-T)(k_eⁱ - kd )(Vd / Ve)

(this formula is given on the formula sheet)

Explanation of terms

V_e and V_d are the market values of equity and debt respectively.

k_d is the (pre tax) return required by the debt holders.

T is the corporation tax rate.

k_eⁱ is the cost of equity in an equivalent ungeared firm.

k_e is the cost of equity in the geared firm.

Test your understanding 2

Moondog Co is a company with a 20:80 debt:equity ratio. Using CAPM, its cost of equity has been calculated as 12%.

It is considering raising some debt finance to change its gearingratio to 25:75 debt to equity. The expected return to debt holders is 4%per annum, and the rate of corporate tax is 30%.

Calculate the theoretical cost of equity in Moondog Co after the refinancing.

3 The cost of debt

Methods of calculating cost of debt

The company's cost of debt is found by taking the return required by debt holders / lenders (k_d) and adjusting it for the tax relief received by the firm as it pays debt interest.

Note on exam terminology

In exam questions you may be given the cost of debt or you may have to calculate it - see below for calculations.

If you are given the "cost of debt", be aware that the cost of debtis normally quoted pre-tax because this is the rate at which thecompanies will pay interest on their borrowings (even though the 'true'cost to them will be net of tax because interest is payable before taxand therefore companies benefit from the 'tax shield').

It can be assumed, therefore, that cost of debt will mean pre-tax cost of debt (k_d) unless it is clearly stated otherwise.

Using the DVM to estimate cost of debt

In paper F9, the cost of debt was generally estimated using the principles of the dividend valuation model.

The use of DVM to estimate cost of debt

As seen above, the basic theory of the DVM is:

The value of a share = the present value of the future dividends discounted at the shareholders' required rate of return

Using the same logic,

The value of a bond = the present value of the future receipts(interest and redemption amount) discounted at the lenders' requiredrate of return.

This theory gives rise to two alternative calculations of k_d (1-T):

Post tax cost of debt

Irredeemable debt

K_d (1-T) = I (1-T) / MV

where

I = the annual interest paid,

T = corporation tax rate,

MV =  the current bond price.

Illustration of method

Mackay Co has some irredeemable, 5% coupon bonds in issue, which are trading at $94.50 per $100 nominal. The tax rate is 30%.

Mackay Co's post tax cost of debt is 5(1-0.30) / 94.50 = 3.7%

Redeemable debt

k_d (1-T) = the Internal Rate of Return (IRR) of

• the bond price
• the interest (net of tax)
• the redemption payment

Illustration of method

Dodgy Co's 6% coupon bonds are currently priced at $89%. The bondsare redeemable at par in 5 years. Corporation tax is 30%. Calculate thepost tax cost of debt.

To calculate IRR, we discount at 2 rates (5% and 10% here) and then interpolate:

PV at 5% = 89 - (6(1-0.30) × 5 yr 5% annuity factor) - (100 × 5 yr 5% discount factor) = -7.58

PV at 10% = 89 - (6(1-0.30) × 5 yr 10% annuity factor) - (100 × 5 yr 10% discount factor) = 10.98

Hence IRR (post tax cost of debt) is approximately 6%

Pre tax cost of debt (or "yield" to the debt holder)

In both the previous examples, the focus was on finding the posttax cost of debt, which is a key component in the company's WACCcalculation.

In order to compute the pre tax cost of debt (sometimes called the yield to the investor) the method is very similar.

For irredeemable debt, the pre tax cost of debt is simply I/MV.

For redeemable debt, the pre tax cost of debt is the IRR of thebond price, the GROSS interest (i.e. pre tax) and the redemptionpayment.

In both cases, the only difference from the above calculations is that interest is now taken pre tax in the formulae.

Credit spread

However, the main technique used in Paper P4 for deriving cost of debt is based on an awareness of credit spread (sometimes referred to as the "default risk premium"), and the formula:

k_d (1-T) = (Risk free rate + Credit spread) (1-T)

The credit spread is a measure of the credit risk associated with acompany. Credit spreads are generally calculated by a credit ratingagency and presented in a table like the one below: To understand howcredit spreads are derived, see the section on how lenders set theirinterest rates at the end of this chapter.

Credit risk, rating agencies and spread

What is credit risk?

Credit or default risk is the uncertainty surrounding a firm’s ability to service its debts and obligations.

It can be defined as the risk borne by a lender that the borrowerwill default either on interest payments, the repayment of the borrowingat the due date or both.

The role of credit rating agencies

If a company wants to assess whether a firm that owes them money islikely to default on the debt, a key source of information is a creditrating agency.

They provide vital information on creditworthiness to:

• potential investors
• regulators of investing bodies
• the firm itself.

The assessment of creditworthiness

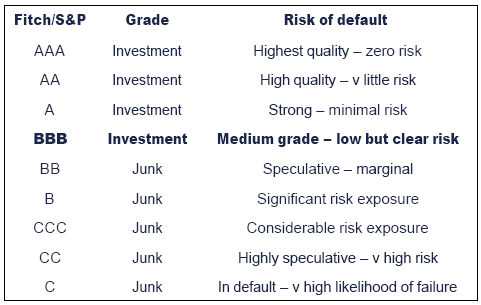
A large number of agencies can provide information on smallerfirms, but for larger firms credit assessments are usually carried outby one of the international credit rating agencies. The three largestinternational agencies are Standard and Poor's, Moodys and Fitch.

Certain factors have been shown to have a particular correlationwith the likelihood that a company will default on its obligations:

• The magnitude and strength of the company’s cash flows.
• The size of the debt relative to the asset value of the firm.
• The volatility of the firm’s asset value.
• The length of time the debt has to run.

Using this and other data, firms are scored and rated on a scale, such as the one shown here:

Calculating credit scores

The credit rating agencies use a variety of models to assess the creditworthiness of companies.

In the popular Kaplan Urwitz model, measures such as firm size,profitability, type of debt, gearing ratios, interest cover and levelsof risk are fed into formulae to generate a credit score.

These scores are then used to create the rankings shown above. For example a score of above 6.76 suggests an AAA rating.

Credit spread

There is no way to tell in advance which firms will default ontheir obligations and which won’t. As a result, to compensate lendersfor this uncertainty, firms generally pay a spread or premium over therisk-free rate of interest, which is proportional to their defaultprobability.

The yield on a corporate bond is therefore given by:

Yield on corporate bond = Yield on equivalent treasury bond + credit spread

Table of credit spreads for industrial company bonds:

Examples of calculations of yield

Simple illustration

The current return on 5-year treasury bonds is 3.6%. C plc hasequivalent bonds in issue but has an A rating. What is the expectedyield on C’s bonds?

Solution

From the table the credit spread for an A rated, 5-year bond is 65.

This means that 0.65% must be added to the yield on equivalent treasury bonds.

So yield on C’s bonds = 3.6% + 0.65% = 4.25%.

More advanced illustration

The current return on 8-year treasury bonds is 4.2%. X plc hasequivalent bonds in issue but has a BBB rating. What is the expectedyield on X’s bonds?

Solution

From the table the credit spread for a BBB rated, 7-year bond is 126. The spread for a 10-year bond is 149.

This would suggest an adjustment of

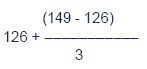
= 126 + 7.67 = 133.67

So 1.34% must be added to the yield on equivalent treasury bonds.

So yield on X’s bonds = 4.2% + 1.34% = 5.54%

Test your understanding 3

The current return on 4-year treasury bonds is 2.6%. F plc has equivalent bonds in issue but has a AA rating.

(i)calculate the expected yield on F’s bonds

(ii) find F’s post tax cost of debt associated with these bonds if the rate of corporation tax is 30%

(Use the information in the table of credit spreads above).

Test your understanding 4

Landline Co has an A credit rating.

It has $30m of 2 year bonds in issue, which are trading at $90%, and $50m of 10 year bonds which are trading at $108%.

The risk free rate is 2.5% and the corporation tax rate is 30%.

Calculate the company's post tax cost of debt capital.

(Use the information in the table of credit spreads above).

Using the CAPM to calculate cost of debt

The CAPM can be used to derive a required return as long as thesystematic risk of an investment is known. Earlier in the chapter we sawhow to use an equity beta to derive a required return on equity. Wealso said that the risk on debt is usually relatively low, so the debtbeta is often zero. However, if the debt beta is not zero (for exampleif the company's credit rating shows that it has a credit spread greaterthan zero) the CAPM can also be used to derive k_d as follows:

kd = R_f + ß_debt (E(R_m) - R_f)

Then, the post tax cost of debt is kd (1-T) as usual.

Test your understanding 5: WACC

An entity has the following information in its balance sheet (statement of financial position):

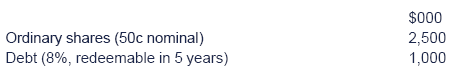
The entity's equity beta is 1.25 and its credit rating according toStandard and Poor's is A. The share price is $1.22 and the debentureprice is $110 per $100 nominal.

Extract from Standard and Poor's credit spread tables:

The risk free rate of interest is 6% and the equity risk premium is 8%. Tax is payable at 30%.

Required:

Calculate the entity's WACC.

Application of Macauley duration to debt

In Chapter 2, we saw how to calculate the Macauley Duration of aninvestment project. The method can also be used to measure thesensitivity of a bond's price to a change in interest rates.

Duration is expressed as a number of years. The bigger the duration, the greater the risk associated with the bond.

Illustration of Macauley Duration calculation for a bond

Tyminski Co has some 10% coupon bonds in issue. They are redeemableat par in 5 years, and are trading at $97.25%. The yield (pre tax costof debt) is 10.743%.

The Macaulay Duration is calculated as follows:

Step 1: Calculate the present value of each future receipt from the bond, using the pre tax cost of debt as the discount rate.

Step 2: Calculate the sum of (time to maturity x PV of receipt)
(1 × 9.03) +(2 × 8.15) +(3 × 7.36) +(4 × 6.66) +(5 × 66.05) = 404.30

Step 3: Divide this by the total PV of receipts (i.e. the bond price) to give the Macauley Duration.

Macauley Duration = 404.30 / 97.25 = 4.157 years

The longer the Macauley Duration, the more volatile the bond.

Benefits and limitations of duration

Benefits

• Duration allows bonds of different maturities and coupon rates to be compared. This makes decision making regarding bond finance easier and more effective.
• If a portfolio of bonds is constructed based on weighted average duration, it is possible to identify the change in value of the portfolio as interest rates change.
• Managers may be able to reduce interest rate risk by changing the overall duration of the bond portfolio (e.g. by adding shorter maturity bonds to reduce duration).

Limitations

The main limitation of duration is that it assumes a linearrelationship between interest rates and bond price. In reality, therelationship is likely to be curvilinear. The extent of the deviationfrom a linear relationship is known as convexity. The more convexthe relationship between interest rates and bond price, the moreinaccurate duration is for measuring interest rate sensitivity.

Further information on convexity

The sensitivity of bond prices to changes in interest rates isdependent on their redemption dates. Bonds which are due to be redeemedat a later date are more price-sensitive to interest rate changes, andtherefore are riskier.

Duration measures the average time it takes for a bond to pay itscoupons and principal and therefore measures the redemption period of abond. It recognises that bonds which pay higher coupons effectivelymature ‘sooner’ compared to bonds which pay lower coupons, even ifthe redemption dates of the bonds are the same. This is because a higherproportion of the higher coupon bonds’ income is received sooner.Therefore these bonds are less sensitive to interest rate changes andwill have a lower duration.

Duration can be used to assess the change in the value of a bond when interest rates change using the following formula:

ΔP = [–D x Δi × P]/[1 + i],

where P is the price of the bond, D is the duration and i is the redemption yield.

However, duration is only useful in assessing small changes in interest rates because of convexity.As interest rates increase, the price of a bond decreases and viceversa, but this decrease is not proportional for coupon paying bonds,the relationship is non-linear. In fact, the relationship between thechanges in bond value to changes in interest rates is in the shape of aconvex curve to origin, see below.

Duration, on the other hand, assumes that the relationship between changes in interest rates and the resultant bond is linear.

Therefore duration will predict a lower price than the actual priceand for large changes in interest rates this difference can besignificant. Duration can only be applied to measure the approximatechange in a bond price due to interest changes, only if changes ininterest rates do not lead to a change in the shape of the yield curve.This is because it is an average measure based on the gross redemptionyield (yield to maturity). However, if the shape of the yield curvechanges, duration can no longer be used to assess the change in bondvalue due to interest rate changes.

4 How do lenders set their interest rates?

Link to credit spreads

The table of credit spreads shown above showed the premium overrisk free rate which a company would have to pay in order to satisfy itslenders. Another way of looking at the issue of yield on a bond is tolook at it from the perspective of the lender. How lenders set theirinterest rates was the subject of an article written by Bob Ryan forStudent Accountant magazine in August 2008.

Overview of the method

Lenders set their interest rates after assessing the likelihoodthat the borrower will default. The basic idea is that the lender willassess the likelihood (using normal distribution theory) of the firm'scash flows falling to a level which is lower than the required interestpayment in the coming year. If it looks likely that the firm will haveto default, the interest rate will be set at a high level to compensatethe lender for this risk.

Introduction to normal distribution theory

The exam formula sheet contains a normal distribution table. Normal distributions have several applications in the P4 syllabus.

A normal distribution is often drawn as a "bell shaped" curve, with its peak at the mean in the centre, as shown:

The figure from the normal distribution table gives the size of anarea (shaded on the diagram) between the mean and a point z standarddeviations away.

Example of a simple normal distribution

The height of adult males is normally distributed with a mean of 175 cm and a standard deviation of 5cm.

What is the probability of a man being shorter than 168cm?

Solution

168cm is 7cm away from the mean.

This represents 7/5 = 1.40 standard deviations.

From tables, 0.4192 of the normal curve lies between the mean and 1.40 standard deviations.

Hence, the probability of a man being shorter than 168cm is 0.5 - 0.4192 = 0.0808 (approximately 8%).

Illustration 1

Villa Co has $2m of debt, on which it pays annual interest of 6%.

The company's operating cash flow in the coming year is forecast tobe $140,000, and currently the company has $12,000 cash on deposit.

Given that the annual volatility (standard deviation) of thecompany's cash flows (measured over the last 5 years) has been 25%,calculate the probability that Villa Co will default on its interestpayment within the next year (assuming that the company has no otherlines of credit available).

Solution

The key here is that Villa Co will have expected cash of $140,000 +$12,000 = $152,000, and its interest commitment will be 6% on $2m, i.e.$120,000.

We need to calculate the probability that the cash available will fall by $152,000 - $120,000 = $32,000 over the next year.

Assuming that the annual cash flow is normally distributed, avolatility (standard deviation) of 25% on a cash flow of $140,000represents a standard deviation of 0.25 × $140,000 = $35,000.

Thus, our fall of $32,000 represents 32,000 / 35,000 = 0.91 standard deviations.

From the normal distribution tables, the area between the mean and 0.91 standard deviations = 0.3186.

Hence, there must be a 0.5 - 0.3186 = 0.1814 chance of the cashflow being insufficient to meet the interest payment.

i.e. the probability of default is approximately 18%.

Calculating the credit spread from this probability of default will be covered in the later chapter on Option Pricing.

5 The use of WACC as a discount rate in project appraisal

Link to project appraisal

When evaluating a project, it is important to use a cost of capitalwhich is appropriate to the risk of the new project. The existing WACCwill therefore be appropriate as a discount rate if both:

(1) the new project has the samelevel of business risk as the existing operations. If business riskchanges, required returns of shareholders will change (to compensatethem for the new level of risk), and hence WACC will change.

(2) undertaking the new projectwill not alter the firm's gearing (financial risk). The values of equityand debt are key components in the calculation of WACC, so if thevalues change, clearly the existing WACC will no longer be applicable.

If one or both of these factors do not apply when undertaking a newproject, the existing WACC cannot be used as a discount rate. The nextchapter explores the alternative methods available in these situations.

6 Chapter overview

Test your understanding answers

Test your understanding 1

In order to use CAPM we shall need to derive a suitable equity beta for Moorland Co.

This will be done by first finding a suitable asset beta (based onthe asset betas of the 2 parts of the business) and gearing up toreflect Moorland Co's 50:50 gearing level.

Retail industry

the asset beta of retail operations can be found from the industry information as follows: (assuming the debt beta is zero)

Manufacturing industry

Similarly, the asset beta for manufacturing operations is:

Moorland Co asset beta

Hence, the asset beta of Moorland will be a weighted average of these two asset betas:

ß _a (Moorland) = (0.75 × 1.02) + (0.25 × 0.92) = 1.00 

Moorland Co equity beta

So, regearing this asset beta now gives:

Moorland Co cost of equity

Using CAPM:

K_e = R_F + ß  (E(R_M) - R_F) = 3% + (1.69 × 6%) = 13.1%

Test your understanding 2

Using M+M's Proposition 2 equation, we can degear the existing k_e and then regear it to the new gearing level:

Degearing:

k_e = k_eⁱ + (1-T)(k_eⁱ - kd )(Vd / Ve)

12% = k_eⁱ+ (1-0.30)(k_eⁱ - 4% )(20 / 80)

Rearranging carefully gives k_eⁱ =10.8%

Now regearing:

k_e = 10.8% + (1-0.30)(10.8%-4%)(25/75)

k_e = 12.4%

Test your understanding 3

From the table the credit spread for an AA rated, 3-year bond is 30. The spread for a 5-year bond is 37.

This would suggest an adjustment of:

The yield is therefore found by adding 0.335% to the yield on equivalent treasury bonds.

So yield on F’s bonds

The cost of debt = 2.935 × (1 – 0.3) = 2.05%

Test your understanding 4

The overall cost of debt will be the weighted average of the costs ofthe two types of debt (weighted according to market values).

2 year bonds

Market value = $30m × 0.90 = $27m

kd = 2.5% + 50 credit spread (from table) = 3.00%

10 year bonds

Market value = $50m × 1.08 = $54m

kd = 2.5% + 75 credit spread (from table) = 3.25%

Overall cost of debt

Therefore the weighted average cost of debt (given that the ratio of market values is 1:2) is

[((1/3) × 3.00%) + ((2/3) × 3.25%)] × (1-0.30) = 2.22%

Test your understanding 5: WACC

Workings:

From CAPM, k_e =R_f + ß_i (E(R_m) - R_f) = 6% + (1.25 × 8%) = 16%

Ve = $2,500,000 × 1.22 / 0.50 = $6.1m

kd (yield on debt) = risk free rate + credit spread = 6% + 65 basis points = 6.65%

Hence, post tax cost of debt = 6.65% (1-0,30) = 4.66%

Vd = $1,000,000 × 110/100 = $1.1m

Therefore, WACC = (6.1 / 7.2) × 16% + (1.1 / 7.2) × 4.66% = 14.3%

Rating :	Ratings & Comments  (Click the stars to rate the page)

Tags: