Chapter 5: Asset investment decisions and capital rationing

Chapter learning objectives

Upon completion of this chapter you will be able to:

• evaluate the choice between leasing an asset and borrowing to buy using the before- and after-tax costs of debt
• define and calculate an equivalent annual cost (EAC)
• evaluate asset replacement decisions using EACs
• explain the reasons why capital rationing might be required
• define and distinguish between divisible and indivisible projects
• calculate profitability indexes for divisible investment projects and use them to evaluate investment decisions
• calculate the net present value (NPV) of combinations of non-divisible investment projects and use the results to evaluate investment decisions.

1 Lease versus buy

Once the decision has been made to acquire an asset for aninvestment project, a decision still needs to be made as to how tofinance it. The choices that we will consider are:

• lease
• buy.

The NPVs of the financing cash flows for both options are found and compared and the lowest cost option selected.

The finance decision is considered separately from the investmentdecision. The operating costs and revenues from the investment will becommon in each case.

Only the relevant cash flows arising as a result of the type of finance are included in the NPV calculation.

Leasing

The asset is never 'owned' by the user company from the perspective of the taxman.

Implications

• The finance company receives the WDAs as the owner of the asset.
• The user receives no WDAs but is able to offset the full rental payment against tax.

The relevant cash flows would thus be:

• the lease payments
• tax relief on the lease payments.

Buying

The assumption is that buying requires the use of a bank loan (forthe sake of comparability). The user is the owner of the asset.

Implication

• The user will receive WDAs on the asset and tax relief for the interest payable on the loan.

The relevant cash flows would be:

• the purchase cost
• any residual value
• any associated tax implications due to WDAs.

Do not include the interest payments or the tax relief arising on themin the NPV calculation, as this is dealt with via the cost of capital(see below).

Cost of capital

As the interest payments attract tax relief we must use thepost-tax cost of borrowing as our discount rate. As all financing cashflows are considered to be risk-free, this rate is used for both leasingand buying.

Post-tax cost of borrowing = Cost of borrowing × (1 –Tax rate).

(Note: in some questions you may find that a company is not paying tax and so the pre-tax rate would be appropriate.)

Lease versus buy

Where the use of an asset is required for a new project, there are effectively two decisions to be made:

• Is the project worthwhile?
• If so, should the asset be leased or bought with a loan?

If the project has been approved in principle then you need tocalculate the NPVs of the two sets of financing cash flows for buyingand leasing.

To be consistent with the earlier calculations, you could use thecompany's existing cost of capital to discount these cash flows.

However, the decision of whether to lease or borrow to buy isactually a financing decision as opposed to an investment decision.Therefore, the appropriate discount rate is the borrowing cost (cost ofdebt) of the company, whether on a before or after-tax basis.

Test your understanding 1 – Leasing calculations

Walshey Co has already decided to accept a project and is now considering how to finance it.

The asset could be leased over four years at a rental of $36,000 pa, payable at the start of each year.

Tax is payable at 30%, one year in arrears. The post-tax cost of borrowing is 10%.

Required:

Calculate the net present value of the leasing option.

Test your understanding 2 – Lease versus buy

A firm has decided to acquire a new machine to neutralise the toxicwaste produced by its refining plant. The machine would cost $6.4million and would have an economic life of five years.

Capital allowances (CAs) of 25% pa on a reducing balance basis are available for the investment.

Taxation of 30% is payable on operating cash flows, one year in arrears.

The firm intends to finance the new plant by means of a five-yearfixed interest loan at a pre-tax cost of 11.4% pa, principal repayablein five years' time.

As an alternative, a leasing company has proposed a finance lease over five years at $1.42 million pa payable in advance.

Scrap value of the machine under each financing alternative will be zero.

Evaluate the two options for acquiring the machine and advise the company on the best alternative.

Other considerations

There may be other issues to consider before a final decision is made to lease or buy, for example:

• Who receives the residual value in the lease agreement?
• Any restrictions associated with the taking on of leased equipment, e.g. leases may restrict a firm's borrowing capacity.
• Any additional benefits associated with lease agreement, e.g. maintenance or other support services.

See chapter 14 for further details.

2 Replacement decisions

Once the decision has been made to acquire an asset for a long-termproject, it is quite likely that the asset will need to be replacedperiodically throughout the life of the project.

Where there are competing replacements for a particular asset we must compare the possible replacement strategies available.

A problem arises where

• equivalent assets available are likely to last for different lengths of time or
• an asset, once bought, must be replaced at regular intervals.

The decision we are concerned with here is – how often should the asset be replaced?

Equivalent annual costs (EACs)

In order to deal with the different time-scales, the NPV of each option is converted into an annuity or an EAC.

The EAC is the equal annual cash flow (annuity) to which a series of uneven cash flows is equivalent in PV terms.

The formula used is:

The optimum replacement period (cycle) will be the period that has the lowest EAC, although in practice other factors may influence the final decision.

 The method can be summarised as:

(1)calculate the NPV of each strategy or replacement cycle

(2)calculate the EAC for each strategy

(3)choose the strategy with the lowest EAC.

Key assumptions

• Cash inflows from trading are ignored since they will be similar regardless of the replacement decision. In practice using an older asset may result in lower quality, which in turn could affect sales.
• The operating efficiency of machines will be similar with differing machines or with machines of differing ages.
• The assets will be replaced in perpetuity or at least into the foreseeable future.
• In most questions tax and inflation are ignored.
• As with all NPV calculations non-financial aspects such as pollution and safety are ignored. An older machine may have a higher chance of employee accidents and may produce more pollution.

Replacement decisions

The factors to be considered when making replacement decisions are as follows:

• Capital cost of new equipment – the higher cost of equipment will have to be balanced against known or possible technical improvements.
• Operating costs – operating costs will be expected to increase as the machinery deteriorates over time. This is referred to as operating inferiority, and is the result of:
  • increased repair and maintenance costs
  • loss of production due to 'down time' resulting from increased repair and maintenance time
  • lower quality and quantity of output.
• Resale value – the extent to which old equipment can be traded in for new.
• Taxation and investment incentives.
• Inflation – both the general price level change, and relative movements in the prices of input and outputs.

Determining the optimum replacement period (cycle) will largely be influenced by:

• the capital cost/resale value of the asset – the longer the period, the less frequently these will occur
• the annual operating costs of running the asset – the longer the period, the higher these will become.

The timescale problems

A special feature of replacement problems is that it involvescomparisons of alternatives with different timescales. If the choice isbetween replacing an item of machinery every two years or every threeyears, it would be meaningless simply to compare the NPV of the twocosts.

Almost certainly P < q.="" however,="" this="" does="" not="" take="" account="" ofthe="" cost="" of="" providing="" an="" asset="" for="" the="" third="" year.="" one="" way="" of="" comparingasset="" replacement="" options="" is="" to="" convert="" the="" pv="" of="" cost="" over="" onereplacement="" cycle="" to="" an="" equivalent="" annual="" pv="" of="">

In other words, we compute the PV of costs over one cycle and thenturn it into an EAC using the AF for the number of years in thereplacement cycle.

Thus, the costs associated with any particular cycle can beconsidered as equivalent to having to pay this EAC every year throughoutthe cycle and throughout subsequent cycles.

Test your understanding 3 – Equivalent annual costs

A machine costs $20,000.

The following information is also available:

Running costs (payable at the end of the year):

Calculate the optimal replacement cycle if the cost of capital is 10%.

Test your understanding 4 – Equivalent annual costs

A decision has to be made on replacement policy for vans. A van costs $12,000 and the following additional information applies:

Calculate the optimal replacement policy at a cost of capital of 15%.

Note that the asset is only maintained at the end of the year if itis to be kept for a further year, i.e. there are no maintenance costsin the year of replacement.

Ignore taxation and inflation.

Limitations of replacement analysis

The model assumes that when an asset is replaced, the replacementis in all practical respects identical to the last one and that thisprocess will continue for the foreseeable future. However in practicethis will not hold true owing to:

• changing technology
• inflation
• changes in production plans.

Limitations of replacement analysis

The replacement analysis model assumes that the firm replaces like with like each time it needs to replace an existing asset.

However this assumption ignores:

• Changing technology – machines fast become obsolete and can only be replaced with a more up-to-date model which will be more efficient and perhaps perform different functions.
• Inflation – the increase in prices over time alters the cost structure of the different assets, meaning that the optimal replacement cycle can vary over time.
• Changes in production plans – firms cannot predict with accuracy the market environment they will be facing in the future and whether they will even need to make use of the asset at that time.

Equivalent annual benefits

The equivalent annual benefit (EAB) is the annual annuity with the same value as the net present value of an investment project.

It can be calculated using a similar formula to that used for the equivalent annual cost:

Calculating the EAB is particularly useful when trying to compareprojects with unequal lives. The project with the highest EAB would bepreferred.

3 Capital rationing

An introduction

Shareholder wealth is maximised if a company undertakes allpossible positive NPV projects. Capital rationing is where there areinsufficient funds to do so. This implies that where investment capitalis rationed, shareholder wealth is not being maximised.

 Ensure you are able to discuss the difference between hard (external) and soft (internal) capital rationing.

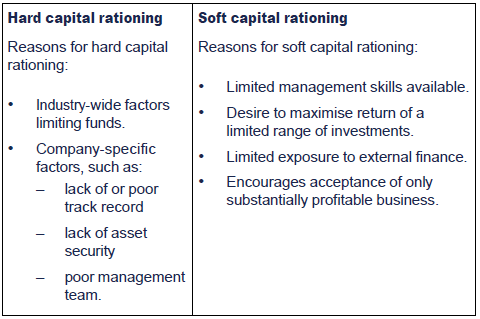
Hard capital rationing: An absolute limit on the amount of finance available is imposed by the lending institutions.

Soft capital rationing: A company may impose its own rationing on capital. This is contrary to the rational view of shareholder wealth maximisation.

Reasons for hard or soft capital rationing

Single and multi-period capital rationing

Single-period capital rationing: Shortage of funds for this period only.

Multi-period capital rationing: Shortage of funds in more than one period (outside syllabus)

The method for dealing with single-period capital rationing issimilar to the limiting factor analysis used elsewhere in decisionmaking.

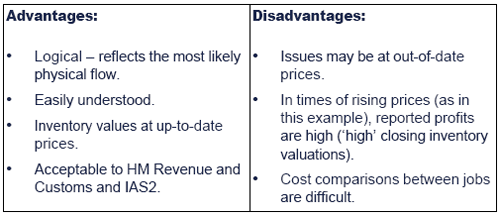
The profitability index (PI) and divisible projects

If a project is divisible, any fraction of the project may beundertaken and the returns from the project are expected to be generatedin exact proportion to the amount of investment undertaken. Projectscannot however be undertaken more than once.

The aim when managing capital rationing is to maximise the NPV earned per $1 invested in projects.

Where the projects:

• are divisible (i.e. can be done in part)
• earn corresponding returns to scale

it is achieved by:

(1)calculating a PI for each project (see below)

(2)ranking the projects according to their PI

(3)allocating funds according to the projects’ rankings until they are used up.

The formula is:

Test your understanding 5 – Divisible projects

A company has $100,000 available for investment and has identifiedthe following 5 investments in which to invest. All investments must bestarted now (Yr 0).

Required:

Determine which projects should be chosen to maximise the return to the business.

Indivisible projects – trial and error

If a project is indivisible it must be done in its entirety or not at all.

Where projects cannot be done in part, the optimal combination can only be found by trial and error.

Test your understanding 6 – Indivisible projects

A Co has the same problem as before but this time the projects are indivisible.

The information is reproduced below:

A company has $100,000 available for investment and has identifiedthe following 5 investments in which to invest. All investments must bestarted now (Yr 0).

Required:

Determine the optimal project selection.

The key in the examination is to ascertain whether or not the projects are divisible.

Divisible projects can be ranked using the PI. Combinations ofindivisible projects must be considered on a trial and error basis.

Mutually-exclusive projects

Sometimes the taking on of projects will preclude the taking on of another, e.g. they may both require use of the same asset.

In these circumstances, each combination of investments is tried to identify which earns the higher level of returns.

Test your understanding 7 – Mutually exclusive projects

Using the same company information for A Co (divisible projects)the additional factor to be considered is that projects C and E aremutually exclusive.

The information is reproduced below.

A company has $100,000 available for investment and has identifiedthe following 5 investments in which to invest. All investments must bestarted now (Yr 0).

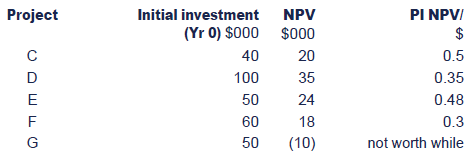
Required:

Determine the optimal project selection.

Chapter summary

Test your understanding answers

Test your understanding 1 – Leasing calculations

Cost of leasing:

• Or 3.170 × 0.909 = 2.882

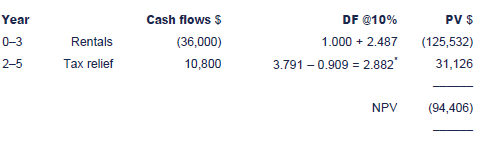
Test your understanding 2 – Lease versus buy

(W1) Calculation of the tax relief on WDAs if asset bought:

Note: The asset is bought at time t=0 as usual with the firstCA in the year ended time one. Given the one-year time lag on the tax,the first tax effect is at time t=2.

(W2) Calculation of the post-tax cost of borrowing.

The pre-tax cost of borrowing is 11.4%.

The post-tax cost of borrowing can be approximated by multiplyingthis by (1 – tax rate), i.e. 11.4% × (1 – 0.3) = 7.98%, say 8%(strictly this ignores the impact of a one-year time delay on taxrelief, but this is acceptable).

Cost of borrowing to buy:

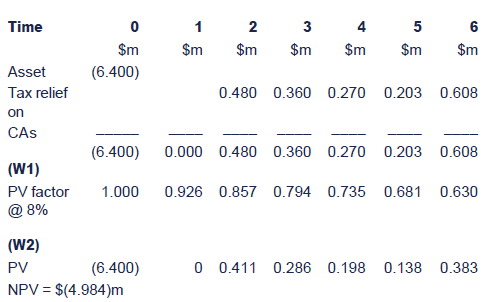
Cost of leasing:

The cost of leasing is lower than the cost of buying and the asset should therefore be acquired under a finance lease.

Test your understanding 3 – Equivalent annual costs

Note: in contrast to the maintenance costs in the aboveillustration, running costs (e.g. petrol) are incurred in every year ofownership.

One-year replacement cycle:

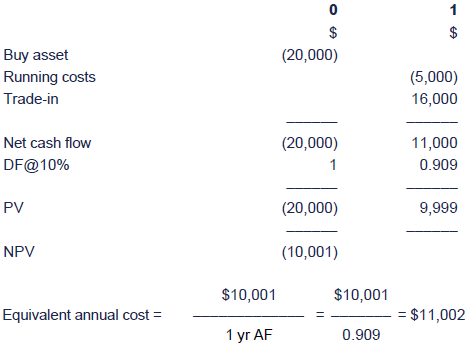
Two-year replacement cycle:

The machine should therefore be replaced after two years.

Test your understanding 4 – Equivalent annual costs

The costs incurred over a single cycle are computed and the EAC is found as follows.

(1)Replace every year

(2)Replace every two years

(3)Replace every three years

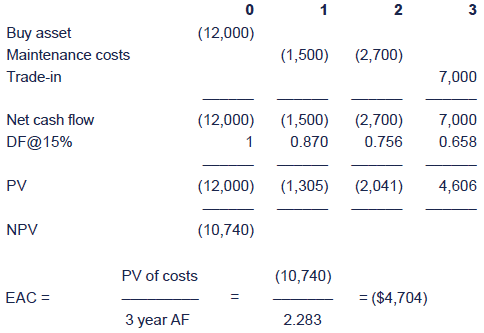
Here, the optimal replacement period is every two years.

Note that the EAC is that sum that could be paid annually inarrears to finance the three replacement cycles. It is equivalent to thebudget accounts that various public services encourage customers toopen to spread the cost of those services more evenly. The PV of annualsums equal to the EAC is the same as the PV of the various receipts andpayments needed to buy and maintain a van.

Test your understanding 5 – Divisible projects

Solution

Test your understanding 6 – Indivisible projects

Solution

^*C and E is the best mix. There is a problem howeverrelating to the unused funds. The assumption is that the un-utilisedfunds will earn a return equivalent to the cost of capital and hencewill generate an NPV of 0. This may or may not be the case.

Test your understanding 7 – Mutually exclusive projects

Solution

^* The best mix

Note that F is not considered as it ranks below project D according to the PI.

Rating :	Ratings & Comments  (Click the stars to rate the page)

Tags: