Chapter 6: Risk and uncertainty
Chapter learning objectives
Upon completion of this chapter you will be able to:
- describe generally available research techniques to reduce uncertainty, e.g. focus groups, market research;
- suggest for a given situation, suitable research techniques for reducing uncertainty;
- explain, using a simple example, the use of simulation;
- explain, calculate and demonstrate the use of expected values and sensitivity analysis in simple decision-making situations;
- for given data, apply the techniques of maximax, maximin and minimax regret to decision making problems including the production of profit tables;
- calculate the value of perfect information;
- calculate the value of imperfect information.
1 Introduction
Risk and uncertainty
All businesses face risk.
Risk is the variability of possible returns.
Risk management is important in a business. It is the process ofunderstanding and managing the risks that an organisation is inevitablysubject to.
Distinction between risk and uncertainty
Risk: there are a number of possible outcomes and the probability of each outcome is known.
For example, based on past experience of digging for oil in aparticular area, an oil company may estimate that they have a 60% chanceof finding oil and a 40% chance of not finding oil.
Uncertainty: there are a number of possible outcomes but the probability of each outcome is not known.
For example, the same oil company may dig for oil in a previouslyunexplored area. The company knows that it is possible for them toeither find or not find oil but it does not know the probabilities ofeach of these outcomes.

 The use of research techniques to reduce uncertainty
The use of research techniques to reduce uncertainty
Market research is an important means of assessing and reducinguncertainty. For example, about the likely responses of customers to newproducts, new advertising campaigns and price changes.
A number of research techniques are available:
- Focus Groups
- Desk research (secondary research).
- Field research (primary research). This includes:
- motivational and
- measurement research.
Each method will be reviewed in turn.
Focus groups
Focus groups are a common market research tool involving smallgroups (typically eight to ten people) selected from the broaderpopulation. The group is interviewed through facilitator-led discussionsin an informal environment in order to gather their opinions andreactions to a particular subject.
For example, a supermarket may use a focus group before a productlaunch decision is made in order to gather opinions on a new range ofpizzas.
Problems with focus groups
- Results are qualitative.
- The small sample size means that results may not be representative.
- Individuals may feel under pressure to agree with other members or to give a 'right' answer.
- Their cost and logistical complexity is frequently cited as a barrier, especially for smaller companies. On-line focus groups are becoming more popular and help to address this issue.
Desk research
- The information is collected from secondary sources.
- It obtains existing data by studying published and other available sources of information. For example, press articles, published accounts, census information.
- It can often eliminate the need for extensive field work.
Factors to consider when using desk research
- It may not be exactly what the researcher wants and may not be totally up to date or accurate.
- However, it is quicker and cheaper than field research.
There are three main types of information that can be collected by desk research:
- Economic intelligence can be defined as information relating to the economic environment within which a company operates. It is concerned with such factors as gross national product (GNP), investment, expenditure, population, employment, productivity and trade. It provides an organisation with a picture of past and future trends in the environment and with an indication of the company's position in the economy as a whole. A great deal of information is freely available in this area from sources such as government ministries, the nationalised industries, universities and organisations such as the OECD.
- Market intelligence is information about a company's present or possible future markets. Such information will be both commercial and technical, for example, the level of sales of competitors' products recorded by the Business Monitor or Census of Production; the product range offered by existing or potential competitors; the number of outlets forming the distribution network for a company's products; the structure of that network by size, location and relation to the end user; and the best overseas markets for a company.
- Internal company data is perhaps the most neglected source of marketing information. Companies tend to record their sales information for accountancy purposes or for the management of the sales force. Conversely, many companies, especially blue-chips and public services, can often be seen to produce reams of data for no apparent reason, or because 'we always have done'. Rarely is the information collected in a form in which it can readily be used by marketing management.
Field research
- Information is collected from primary sources by direct contact with a targeted group.
- Although it is more expensive and time consuming than desk research the results should be more accurate, relevant and up to date.
- There are two types of field research:
- motivational research
- measurement research.
Motivational research – the objective is to understand factors that influence why consumers do or do not buy particular products.


 Motivational research techniques
Motivational research techniques
Some of the more common techniques in motivational research are:
- Depth interviewing – undertaken at length by a trained person who is able to appreciate conscious and unconscious associations and motivations and their significance.
- Group interviewing – where between six and ten people are asked to consider the relevant subject (object) under trained supervision.
- Word association testing – on being given a word by the interviewer, the first word that comes into the mind of the person being tested is noted.
- Triad testing – where people are asked which out of a given three items they prefer. If the three are brands of a given type of product (or three similar types), replies may show a great deal about which features of a product most influence the buying decision.
Measurement research – the objective here is to build on the motivation research by trying to quantify the issues involved.
- Sample surveys are used to find out how many people buy the product, what quantity each type of buyer purchases, and where and when the product is bought.
- This sort of information can also be collected in retail environments at the point of sale, for example, through the use of loyalty cards.


 Types of measurement research
Types of measurement research
It is also possible (less accurately) to assess roughly theimportance of some reasons for buying or not buying a product. The maintypes of measurement are:
Random sampling– where each person in the targetpopulation has an equal chance of being selected. Such samples are morelikely to be representative, making predictions more reliable. However,the technique may be unfeasible in practice.
Quota sampling– where samples are designed to be representative with respect to pre-selected criteria.
- For example, if the target population is 55% women and 45% men, then a sample of 200 people could be structured so 110 women and 90 men are asked, rather than simply asking 200 people and leaving it up to chance whether or not the gender mix is typical.
- The main disadvantage of quota sampling is that samples may still be biased for non-selected criteria.
Panelling– where the sample is kept for subsequent investigations, so trends are easier to spot.
Surveying by post– the mail shot method. Unfortunately the sample becomes self-selecting and so may be biased.
Observation– e.g. through the use of cameras withinsupermarkets to examine how long customers spend on reading thenutritional information on food packaging.

2 Other methods of dealing with risk and uncertainty
In addition to the research techniques discussed, the following methods can be used to address risk or uncertainty.
- Sensitivity analysis
- Simulation
- Expected values
- Maximax, maximin and minimax regret
- Decision Trees
Each method will be reviewed in turn.
 3 Sensitivity analysis
3 Sensitivity analysis
Sensitivity analysis takes each uncertain factor in turn, andcalculates the change that would be necessary in that factor before theoriginal decision is reversed. Typically, it involves posing 'what-if'questions.
By using this technique it is possible to establish which estimates(variables) are more critical than others in affecting a decision.
The process is as follows:
- Best estimates for variables are made and a decision arrived at.
- Each of the variables is analysed in turn to see how much the original estimate can change before the original decision is reversed. For example, it may be that the estimated selling price can fall by 5% before the original decision to accept a project is reversed.
- Estimates for each variable can then be reconsidered to assess the likelihood of the estimate being wrong. For example, what is the chance of the selling price falling by more than 5%?
- The maximum possible change is often expressed as a percentage.This formula only works for total cash flows. It cannot be used for individual units, selling prices, variable cost per unit, etc.

 Illustration 1 - Sensitivity analysis
Illustration 1 - Sensitivity analysis
A manager is considering a make v buy decision based on the following estimates:
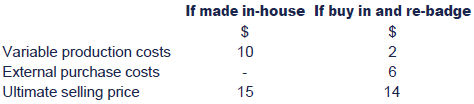
You are required to assess the sensitivity of the decision to the external purchase price.
Solution
Step 1: What is the original decision?
Comparing contribution figures, the product should be bought in and re-badged:

Step 2: Calculate the sensitivity (to the external purchase price)
For indifference, the contribution from outsourcing needs to fallto $5 per unit. Thus the external purchase price only needs to increaseby $1 per unit (or $1/ $6 = 17%). If the external purchase price rose bymore than 17% the original decision would be reversed.

Strengths of sensitivity analysis
- There is no complicated theory to understand.
- Information will be presented to management in a form which facilitates subjective judgement to decide the likelihood of the various possible outcomes considered.
- It identifies areas which are crucial to the success of the project. If the project is chosen, those areas can be carefully monitored.
4 Weaknesses of sensitivity analysis
- It assumes that changes to variables can be made independently, e.g. material prices will change independently of other variables. Simulation allows us to change more than one variable at a time.
- It only identifies how far a variable needs to change; it does not look at the probability of such a change.
- It provides information on the basis of which decisions can be made but it does not point to the correct decision directly.
5 Simulation
Simulation is a modelling technique that shows the effect of more than one variable changing at the same time.
It is often used in capital investment appraisal.
The Monte Carlo simulation method uses random numbers andprobability statistics. It can include all random events that mightaffect the success or failure of a proposed project - for example,changes in material prices, labour rates, market size, selling price,investment costs or inflation.
The model identifies key variables in a decision : costs andrevenues, say. Random numbers are then assigned to each variable in aproportion in accordance with the underlying probability distribution.For example, if the most likely outcomes are thought to have a 50%probability, optimistic outcomes a 30% probability and pessimisticoutcomes a 20% probability, random numbers, representing thoseattributes, can be assigned to costs and revenues in those proportions.
A powerful computer is then used to repeat the decision many timesand give management a view of the likely range and level of outcomes.Depending on the management's attitude to risk, a more informed decisioncan be taken.
This helps to model what is essentially a one-off decision usingmany possible repetitions. It is only of any real value, however, if theunderlying probability distribution can be estimated with some degreeof confidence.

 Illustration 2 - The MP Organisation
Illustration 2 - The MP Organisation
The MP Organisation is an independent film production company. Ithas a number of potential films that it is considering producing, one ofwhich is the subject of a management meeting next week. The film whichhas been code named CA45 is a thriller based on a novel by a wellrespected author.
The expected revenues from the film have been estimated as follows:there is a 30% chance it may generate total sales of $254,000; 50%chance sales may reach $318,000 and 20% chance they may reach $382,000.
Expected costs (advertising, promotion and marketing) have alsobeen estimated as follows: there is a 20% chance they will reachapproximately $248,000; 60% chance they may get to $260,000 and 20 %chance of totalling $272,000.
In a Monte Carlo simulation, these revenues and costs could have random numbers assigned to them:

A computer could generate 20-digit random numbers such as98125602386617556398. These would then be matched to the random numbersassigned to each probability and values assigned to 'Sales Revenues' and'Costs' based on this. The random numbers generated give 5 possibleoutcomes in our example:
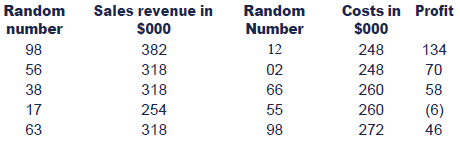


 Illustration 3 - Simulation
Illustration 3 - Simulation
A business is choosing between two projects, project A and projectB. It uses simulation to generate a distribution of profits for eachproject.
Required:
Which project should the business invest in?
Solution
Project A has a lower average profit but is also less risky (less variability of possible profits).
Project B has a higher average profit but is also more risky (more variability of possible profits).
There is no correct answer. All simulation will do is give thebusiness the above results. It will not tell the business which is thebetter project.
If the business is willing to take on risk, they may prefer project B since it has the higher average return.
However, if the business would prefer to minimise its exposure torisk, it would take on project A. This has a lower risk but also a loweraverage return.

Drawbacks of simulation
There are major drawbacks of simulation:
- It is not a technique for making a decision, only for obtaining more information about the possible outcomes.
- Models can become extremely complex.
- The time and costs involved in their construction can be more than is gained from the improved decisions.
- Probability distributions may be difficult to formulate.

 Test your understanding 1
Test your understanding 1
Assess the use of simulation for a chain of betting shops.

6 Expected values (EVs)
An expected value is a weighted average of all possible outcomes.It calculates the average return that will be made if a decision isrepeated again and again. In other words, it is obtained by multiplyingthe value of each possible outcome (x), by the probability of thatoutcome (p), and summing the results.
The formula for the expected value is EV = Σpx

 Illustration 4 – Calculating EVs
Illustration 4 – Calculating EVs
Returns from a new restaurant venture depend on whether acompetitor decides to open up in the same area. The following estimatesare made:


Since the expected value shows the long run average outcome of adecision which is repeated time and time again, it is a useful decisionrule for a risk neutral decision maker. This is because a risk neutral investor neither seeks risk or avoids it; he is happy to accept an average outcome.
Advantages and disadvantages of EVs
Advantages:
- Takes uncertainty into account by considering the probability of each possible outcome and using this information to calculate an expected value.
- The information is reduced to a single number resulting in easier decisions.
- Calculations are relatively simple.
Disadvantages:
- The probabilities used are usually very subjective.
- The EV is merely a weighted average and therefore has little meaning for a one-off project.
- The EV gives no indication of the dispersion of possible outcomes about the EV, i.e. the risk.
- The EV may not correspond to any of the actual possible outcomes.
Pay-off tables
A profit table (pay-off table) can be a useful way to represent andanalyse a scenario where there is a range of possible outcomes and avariety of possible responses. A pay-off table simply illustrates allpossible profits/losses.

 Illustration 5 - Geoffrey Ramsbottom
Illustration 5 - Geoffrey Ramsbottom
Geoffrey Ramsbottom runs a kitchen that provides food for variouscanteens throughout a large organisation. A particular salad is sold tothe canteen for $10 and costs $8 to prepare. Therefore, the contributionper salad is $2.
Based upon past demands, it is expected that, during the 250-dayworking year, the canteens will require the following daily quantities:

The kitchen must prepare the salad in batches of 10 meals. Itsstaff has asked you to help them decide how many salads it should supplyfor each day of the forthcoming year.


 Solution - Geoffrey Ramsbottom
Solution - Geoffrey Ramsbottom
Constructing a pay-off table:
- If 40 salads will be required on 25 days of a 250-day year, the probability that demand = 40 salads is :
P(Demand of 40) = 25 days ÷ 250 days
P(Demand of 40) = 0.1
- Likewise, P(Demand of 50) = 0 .20; P(Demand of 60 = 0.4) and P(Demand of 70 = 0.30).
- Now let's look at the different values of profit or losses depending on how many salads are supplied and sold. For example, if we supply 40 salads and all are sold, our profits amount to 40 x $2 = 80.
- If however we supply 50 salads but only 40 are sold, our profits will amount to 40 x $2 - (10 unsold salads x $8 unit cost) = 0.
We can now construct a pay-off table as follows:


7 Maximax, maximin and minimax regret
When probabilities are not available, there are still tools available for incorporating uncertainty into decision making.
Maximax
 The maximax rule involves selecting the alternative that maximises the maximum pay-off achievable.
The maximax rule involves selecting the alternative that maximises the maximum pay-off achievable.
This approach would be suitable for an optimist, or 'risk-seeking'investor, who seeks to achieve the best results if the best happens.

 Illustration 6 - The Maximax rule
Illustration 6 - The Maximax rule
Following up from the pay-off table example, Geoffrey Ramsbottom's table looks as follows:
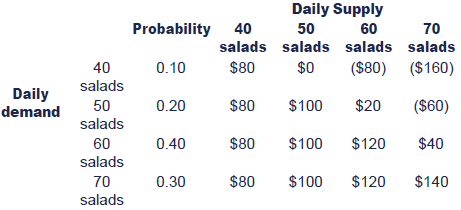
The manager who employs the maximax criterion is assuming thatwhatever action is taken, the best will happen; he/she is a risk-taker.How many salads will he decide to supply?


 Answer
Answer
Here, the highest maximum possible pay-off is $140. We should therefore decide to supply 70 salads a day.


 Test your understanding 2 - Applying maximax
Test your understanding 2 - Applying maximax
A company is choosing which of three new products to make (A, B orC) and has calculated likely pay-offs under three possible scenarios (I,II or III), giving the following pay-off table.
Required:
Using maximax, which product would be chosen?

 Maximin
Maximin
The maximin rule involves selecting the alternative that maximisesthe minimum pay-off achievable. The investor would look at the worstpossible outcome at each supply level, then selects the highest one ofthese. The decision maker therefore chooses the outcome which isguaranteed to minimise his losses. In the process, he loses out on theopportunity of making big profits.
This approach would be appropriate for a pessimist who seeks to achieve the best results if the worst happens.

 Test your understanding 3 - Applying maximin
Test your understanding 3 - Applying maximin
Required:
Using the information from the previous TYU apply the maximin rule to decide which product should be made.


 Illustration 7 - The 'Maximin' rule
Illustration 7 - The 'Maximin' rule
Following up from the pay-off table example, Geoffrey Ramsbottom's table looks as follows:
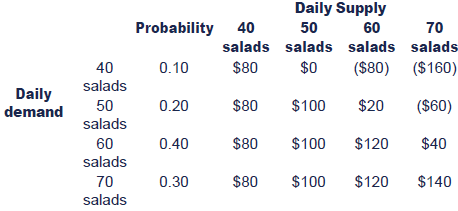
How many salads should we supply, using the Maximin rule?


 Answer
Answer
If we decide to supply 40 salads, the minimum pay-off is $80.
If we decide to supply 50 salads, the minimum pay-off is $0.
If we decide to supply 60 salads, the minimum pay-off is ($80).
If we decide to supply 70 salads, the minimum pay-off is ($160).
The highest minimum payoff arises from supplying 40 salads.

The minimax regret rule
 The minimax regret strategy is the one that minimises the maximumregret. It is useful for a risk-neutral decision maker. Essentially,this is the technique for a ‘sore loser' who does not wish to make thewrong decision.
The minimax regret strategy is the one that minimises the maximumregret. It is useful for a risk-neutral decision maker. Essentially,this is the technique for a ‘sore loser' who does not wish to make thewrong decision.
‘Regret' in this context is defined as the opportunity loss through havingmade the wrong decision.

 Illustration 8 - The 'Minimax Regret' rule
Illustration 8 - The 'Minimax Regret' rule
Following up from the pay-off table example, Geoffrey Ramsbottom's table looks as follows :
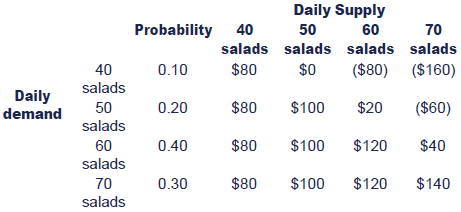
How many salads should we decide to supply if the minimax regret rule is applied?


 Answer
Answer
Following up from the pay-off table example, Geoffrey Ramsbottom's table looks as follows :
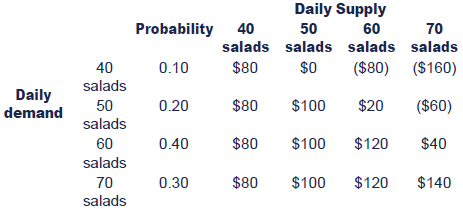
If the minimax regret rule is applied to decide how many saladsshould be made each day, we need to calculate the 'regrets'. This meanswe need to find the biggest pay-off for each demand row, then subtractall other numbers in this row from the largest number.
For example, if the demand is 40 salads, we will make a maximumprofit of $80 if they all sell. If we had decided to supply 50 salads,we would achieve a nil profit. The difference, or 'regret' between thatnil profit and the maximum of $80 achievable for that row is $80.
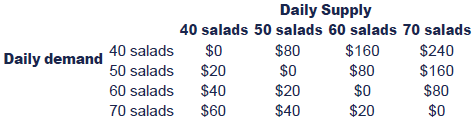
Regrets can be tabulated as follows:
Conclusion
If we decide to supply 40 salads, the maximum regret is $60. If wedecide to supply 50 salads, the maximum regret is $80. For 60 salads,the maximum regret is $160, and $240 for 70 salads. A manager employingthe minimax regret criterion would want to minimise that maximum regret,and therefore supply 40 salads only.

8 Decision trees
A decision tree is a diagrammatic representation of amulti-decision problem, where all possible courses of action arerepresented, and every possible outcome of each course of action isshown.
Decision trees should be used where a problem involves a series ofdecisions being made and several outcomes arise during thedecision-making process. Decision trees force the decision maker toconsider the logical sequence of events. A complex problem is brokendown into smaller, easier to handle sections.
The financial outcomes and probabilities are shown separately, andthe decision tree is ‘rolled back' by calculating expected values andmakingdecisions.
Three step method
Step 1: Draw the tree from left to right, showing appropriate decisions and events / outcomes.
Some common symbols can be used: a square is used to represent a decision point (i.e. where a choice between different courses of action must be taken. A circle is used to represent a chance point. The branches coming away from a circle with have probabilities attached to them. All probabilities should add up to '1'.
Label the tree and relevant cash inflows/outflows and probabilities associated with outcomes.
Step2: Evaluate the tree from right to left carrying out these two actions:
(a) Calculate an EV at each outcome point.
(b) Choose the best option at each decision point.
Step 3: Recommend a course of action to management.

 Decision trees
Decision trees
A university is trying to decide whether or not to advertise a new post-graduate degree programme.
The number of students starting the programme is dependent on economic conditions:
- If conditions are poor it is expected that the programme will attract 40 students without advertising. There is a 60% chance that economic conditions will be poor.
- If economic conditions are good it is expected that the programme will attract only 20 students without advertising. There is a 40% chance that economic conditions will be good.
If the programme is advertised and economic conditions are poor,there is a 65% chance that the advertising will stimulate further demandand student numbers will increase to 50. If economic conditions aregood there is a 25% chance the advertising will stimulate further demandand numbers will increase to 25 students.
The profit expected, before deducting the cost of advertising, at different levels of student numbers are as follows:
Required:
Demonstrate, using a decision tree, whether the programme should be advertised.


 Answer - University advertising decision tree
Answer - University advertising decision tree
Step 1: Draw the tree from left to right. A square is used to represent a decision point (i.e. whether to advertise the programme, or not advertise.).
For both options, a circle is used to represent a chance point - a poor economic environment, or a good economic environment.
Label the tree and relevant cash inflows/outflows and probabilities associated with outcomes :
Step2: Evaluate the tree from right to left carrying out these two actions:
(a) Calculate an Expected Value at each outcome point. Working from top to bottom, we can calculate the EVs as follows:
EV (Outcome Point A) = (35% x $100,000) + (65% x $150,000) = $132,500
EV (Outcome Point B) = (0% x $0) + (25% x $25,000) = $6,250
EV (Outcome Point C) = (60% x $115,000) + (40% x $15,000) = $75,000
EV (Outcome Point D) = (60% x $132,500) + (40% x $6,250) = $82,000
(b) Choose the best option at each decision point and recommend a course of action to management.
At the first (and only) decision point in our tree, we shouldchoose the option to advertise as EV ('D') is $82,000 and EV ('C) is$75,000.

9 The value of perfect information
In many questions the decision makers receive a forecast of afuture outcome (for example a market research group may predict theforthcoming demand for a product). This forecast may turn out to becorrect or incorrect. The question often requires the candidate tocalculate the value of the forecast.
Perfect information The forecast of the future outcome isalways a correct prediction. If a firm can obtain a 100% accurateprediction they will always be able to undertake the most beneficialcourse of action for that prediction.
Imperfect information The forecast is usually correct, but can be incorrect. Imperfect information is not as valuable as perfect information.
The value of information (either perfect or imperfect) may be calculated as follows:
Expected Profit (Outcome) WITH the information LESS Expected Profit (Outcome) WITHOUT the information

 Test your understanding 4 - Geoffrey Ramsbottom
Test your understanding 4 - Geoffrey Ramsbottom
A new ordering system is being considered, whereby customers mustorder their salad online the day before. With this new system MrRamsbottom will know for certain the daily demand 24 hours in advance.He can adjust production levels on a daily basis.
How much is this new system worth to Mr Ramsbottom?

10 The value of imperfect information
Perfect information is only rarely accessible. In fact, informationsources such as market research or industry experts are usually subjectto error. Market research findings, for example, are likely to bereasonably accurate - but they can still be wrong.
Therefore, our analysis must extend to deal with imperfect information. The question is as follows : how much would it be worth paying for such imperfect information, given that we are aware of how right or wrong it is likely to be?

 The Value of Imperfect Information
The Value of Imperfect Information
(a)You have the mineral rights to a piece ofland that you believe may have oil underground. There is only a 10%chance that you will strike oil if you drill, but the profit is$200,000.
It costs $10,000 to drill. The alternative is not to drill at all, in which case your profit is zero.
Should you drill? Draw a decision tree to represent your problem.
(b)Before you drill, you may consult ageologist who can assess the promise of the piece of land. She can tellyou whether the prospects are good or poor, but she is not a perfectpredictor. If there is oil, the probability that she will say there aregood prospects is 95%. If there is no oil, the probability that she willsay prospects are poor is 85%.
Draw a decision tree and calculate the value of imperfectinformation for this geologist. If the geologist charges $7,000, wouldyou use her services?


 Solution
Solution
(a)
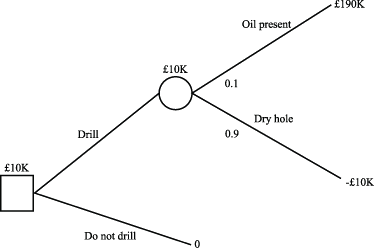
EV ('Drill') = ($190K x 0.1) + (-$10K x 0.9) so EV ('Drill') = $10K.
We should drill, because the expected value from drilling is $10K, versus nothing for not drilling.
(b) We will calculate the Expected Value of profits if we employ the geologist.
If this exceeds $10,000, the geologist would be worth employing as long as the benefit of employing her exceeds her charge of $7,000.
If we employ the geologist, the probabilities of her possibleassessments can be tabulated as follows (assume 1,000 drills in total):
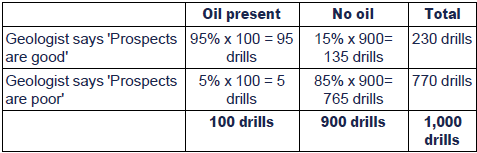
A decision tree can be drawn to calculate the expected value of profits if a geologist is employed:
Working from right to left:
EV(A) = (41.30% x $200,000) - $10,000 drilling costs = $72,600.The decision at 'C' should be to drill, as this generates higherbenefits than not drilling.
EV(B) = (0.65% x $200,000) - $10,000 drilling costs = -$8,700. The decision at 'D' should be not to drill.
EV(E) = 0.23 x $72,600 = $16,698. This is the expected value ofprofits if a geologist is employed and exceeds the EV of profits if sheis not employed.
Expected Value of Imperfect Information = $16,698 - $10,000 =$6,698. Since this is less than the cost of buying the information($7,000), we should not employ the geologist.

11 Chapter summary
Test your understanding answers

 Test your understanding 1
Test your understanding 1
Simulation would be particularly useful on an operational level foranalysing the possible implications of a single event, such as a majorhorse race or football match:
- Possible outcomes are easy to identify (e.g. win, lose, draw, 2-1,3-0, etc)
- Quoted odds can help estimate probabilities
- The outcomes of the simulation could be used to assess impact on cash flow, whether bets should be laid off with other betting agents to reduces risk, etc
Simulation could also be used for wider strategic analysis such asfor assessing the possibility and implications of stricter anti-gamblinglegislation.


 Test your understanding 2 - Applying maximax
Test your understanding 2 - Applying maximax
Using maximax, an optimist would consider the best possible outcomefor each product and pick the product with the greatest potential.
Here C would be chosen with a maximum possible gain of 100.


 Test your understanding 3 - Applying maximin
Test your understanding 3 - Applying maximin
- Using maximin, a pessimist would consider the poorest possible outcome for each product and would ensure that the maximum pay-off is achieved if the worst result were to happen.
- Therefore, product A would be chosen resulting in a minimum pay-off of 20 compared to a minimum pay-off of 10 for products B and C.


 Test your understanding 4 - Geoffrey Ramsbottom
Test your understanding 4 - Geoffrey Ramsbottom

Working 1 :
According to the pay-off table from Illustration 5, the Expected Value of Profits if 40 salads are supplied can be calculated as (0.10 x $80) + (0.20 x $80) + (0.40 x $80) + (0.30 x $80) = $80.
Likewise :

Profits are therefore maximised at 50 salads and amount to $90.

|
Created at 5/24/2012 4:39 PM by System Account
(GMT) Greenwich Mean Time : Dublin, Edinburgh, Lisbon, London
|
Last modified at 5/25/2012 12:54 PM by System Account
(GMT) Greenwich Mean Time : Dublin, Edinburgh, Lisbon, London
|
|
|
|
 |
Rating
:
|
 Ratings & Comments
(Click the stars to rate the page) Ratings & Comments
(Click the stars to rate the page)
|
 |
Tags:
|
|