Chapter 8: Quantitative analysis
Chapter learning objectives
Upon completion of this chapter you will be able to:
- explain and evaluate the use of high/low analysis to separate the fixed and variable elements of total cost
- explain and evaluate the use of regression analysis to separate the fixed and variable elements of total cost
- explain the use of time series analysis as a forecasting technique
- predict a future value from time series analysis data using both the additive and proportional data
- explain the use of a simple average growth model as a forecasting technique
- explain the use of judgement and experience in forecasting
- explain the learning curve effect
- estimate the learning effect and apply this to a budgetary problem
- calculate production times when the learning curve has reached a steady state
- explain the limitations of the learning curve model.
1 High/low analysis
 A method of analysing a semi-variable cost into its fixed and variableelements based on an analysis of historical information about costs atdifferent activity levels.
A method of analysing a semi-variable cost into its fixed and variableelements based on an analysis of historical information about costs atdifferent activity levels.
The fixed and variable costs can then be used to forecast the total cost at any level of activity.
The approach is as follows:
Step 1
Select the highest and lowest activity levels, and their costs.
Step 2
Find the variable cost/unit.
Variable cost/unit = (Cost at high level of activity – Cost atlow level activity)/(High level activity – Low level activity)
Step 3
Find the fixed cost, using either the high or low activity level.
Fixed cost = Total cost at activity level — Total variable cost
Step 4
Use the variable and fixed cost to forecast the total cost for a specified level of activity.
Advantages of high/ low analysis
- The high-low method has the enormous advantage of simplicity.
- It is easy to understand and easy to use.
Disadvantages of high/ low analysis
- It assumes that activity is the only factor affecting costs.
- It assumes that historical costs reliably predict future costs.
- It uses only two values, the highest and the lowest, so the results may be distorted due to random variations in these values.

 Test your understanding 1
Test your understanding 1
Cost data for the six months to 31 December 20X8 is as follows:

Required:
Use high/low analysis to find the variable cost per unit and thetotal fixed cost. Forecast the total cost when 500 units are produced.


 Additional example on high/low
Additional example on high/low
(a) Find the variable cost per unit.
(b) Find the total fixed cost.
(c) Estimate the total cost if output is 350 units.
(d) Estimate the total cost if output is 600 units.
Solution
(a) Variable cost per unit = ($9,000 – $7,000) ÷ (400 – 200)
= $10 per unit
(b) Using high activity level:
(c) If output is 350 units:
(d) If output is 600 units:

2 Regression analysis
Introduction
 Regression is another method of forecasting. It involves usinghistorical data to find the line of best fit between two variables (onedependent on the other), and uses this straight line to predict futurevalues.
Regression is another method of forecasting. It involves usinghistorical data to find the line of best fit between two variables (onedependent on the other), and uses this straight line to predict futurevalues.
A scatter diagram can be drawn:
The dependent variable is y and must always be on the vertical axis, e.g. sales.
The independent variable is x and always goes on the horizontal axis, e.g. advertising spend.
Scatter diagram
The aim is to find the best line (the ‘line of best fit') through the centre of this diagram.
This straight line can then be used for forecasting, e.g. to forecast sales for any level of advertising spend.
Equation of a straight line
The equation of a straight line is y = a + bx
(a) is the intercept with the y axis
(b) is the gradient or slope
It can be time consuming to find the values of 'a' and 'b' bydrawing the scatter diagram. Instead, the following formulae can be usedto find these values.

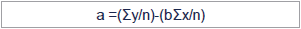
where n = sample size
Both of these formulae are given in the examination.

 Test your understanding 2
Test your understanding 2
A company has recorded expenditure on advertising and resulting sales for six months as follows:

Required:
(a) Plot the data on a scatter diagram and comment.
(b) Calculate the values of 'a' and 'b' and comment.
(c) What is the equation of the line of best fit?
(d) Forecast sales when advertising expenditure is:
(i)$50,000
(ii) $100,000
and comment on your answers.


 Additional example on regression analysis
Additional example on regression analysis
Regression analysis is being used to find the line of best fit (y =a + bx) from 11 pairs of data. The calculations have produced thefollowing information:
∑x = 440, ∑y = 330, ∑x2= 17,986, ∑y2= 10,366 and ∑xy = 13,467
Required:
(a) Find the equation of the line of best fit using regression analysis.
(b) Use your equation to forecast the value of y if x = 42.
Solution
(a) Use the formulae to find the values of a and b.
b = [11 × 13,467 — (440 × 330)]/[(11 × 17,986) — (440)2]= 0.6917
a = (330 ÷ 11) — 0.6917 (440 ÷ 11) = 2.33
The equation of the line is y = 2.33 + 0.6917x
(b) If x = 42, y = 2.33 + 0.6917 × 42 = 31.38 (to 2 decimal points)

Correlation coefficient
The strength of the linear relationship between the two variables(and hence the usefulness of the regression line equation) can beassessed by calculating the correlation coefficient (“râ€):
The correlation coefficient will be between -1 and +1.
- r is close to +1: there is a strong positive correlation between the two variables
- r is close to –1: there is a strong negative correlation between the two variables
- r is close to 0: there is little relationship between the two variables
The closer the coefficient is to +1 or –1, the better regression analysis will be as a method of forecasting.
Using the data from the previous test your understanding:
Coefficient of determination
The coefficient of determination = r2
It shows the percentage change in the dependent variable, e.g.sales, that can be explained by a change in the independent variable,e.g. advertising spend.
Using the data from the previous test your understanding:
r2 = 0.957
Thus 95.7% of the observed variation in sales can be explained asbeing due to changes in the advertising spend. This would give strongassurances that the forecasts made using the regression equation arevalid.
3 Time series analysis
 A time series is a series of figures relating to the changing value of avariable over time. The data often conforms to a certain pattern overtime. This pattern can be extrapolated into the future and henceforecasts are possible. Time periods may be any measure of timeincluding days, weeks, months and quarters.
A time series is a series of figures relating to the changing value of avariable over time. The data often conforms to a certain pattern overtime. This pattern can be extrapolated into the future and henceforecasts are possible. Time periods may be any measure of timeincluding days, weeks, months and quarters.
Components of a time series
- The trend – this describes the long-term general movement of the data.
- Seasonal variations – a regular variation around the trend over a fixed time period.
- Cyclical variations – economic cycle of booms and slumps.
- Residual variations – irregular, random fluctuations in the data usually caused by factors specific to the time series. They are unpredictable.
In examination problems there is generally insufficient data toevaluate the cyclical and residual variations, hence, they are ignored.
The numerical analysis
- The trend and the seasonal variation will be given in the exam.
- These can be combined, using either the additive or the multiplicative model, and used to forecast future values.
The additive model
Actual = Trend + Seasonal Variation (SV)
The SV will be expressed in absolute terms.
The multiplicative model
Actual = Trend × SV factor
The SV will be expressed as a percentage, a decimal or an index.

 Test your understanding 3
Test your understanding 3
A company has found that the trend in the quarterly sales of its furniture is well described by the regression equation

Based on the multiplicative model the mean seasonal quarterly index for its furniture sales is as follows:

Required:
(a) Explain the meaning of this regression equation, and set of seasonal index numbers.
(b) Using the regression equation, estimate the trend values in the company's furniture sales for each quarter of 20X7
(c) Using the seasonal index, prepare sales forecasts for the company's quarterly furniture sales in 20X7
(d) State what factors might cause your sales forecasts to be in error.


 Additional example on time series
Additional example on time series
The number of customers visiting a health centre has beenincreasing and it is estimated that the underlying trend is for anincrease of 50 customers each month. However, the numbers fluctuatedepending on the month of the year.
The underlying trend value for customers in December Year 1 is 4,300.
SVs for some of the months are:

Required:
Prepare a forecast for the number of customers in each of the months May to September, Year 2.
Solution


4 Average growth models
Strategic plans may incorporate an objective of a target averagegrowth of profit or sales over a number of years. There may also berequirements for a target average growth rate of productivity over anumber of years.
g = average growth rate, as a decimal
n = number of periods of growth

 Test your understanding 4
Test your understanding 4
Sales are forecast to increase, on average, by 2% per quarter. Sales are currently $250,000 pa.
Required:
Calculate the budgeted sales figures for each quarter of the forthcoming year.
Calculate the average growth rate given the original and the final figure.

5 The use of judgement and experience in forecasting
Judgement and experience are important in forecasting. Thequantitative models available are mainly based on past information andextrapolate these results into the future. Managers will have access tomany sources of information to help them judge whether past results arelikely to be good predictors of future results.

 Illustration 1 – Judgement and experience in forecasting
Illustration 1 – Judgement and experience in forecasting
A regression analysis has been carried out linking sales toadvertising expenditure. Managers may use their judgement to modify theforecasts if they know that, for example:
- a competitor has recently launched a new product in the market
- a new advertising medium is to be used
- general forecasts of growth in the economy are less favourable
- consumers view the product as being almost out of date.
Managers may:
- forecast more than one scenario to give a most likely, a pessimistic and an optimistic scenario
- use probabilities, estimated using their own judgement and experience, to determine the expected value of a forecast.


 Test your understanding 5
Test your understanding 5
A manager has forecast the following sales revenues and probabilities based on a given level of advertising.
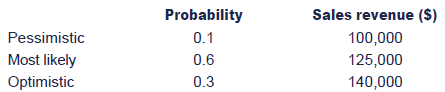
Required:
Calculate the expected value of sales.

6 Learning curves
Introduction
As workers become more familiar with the production of a new product, average time (and average cost) per unit will decline.
 Wrights Law:as cumulative output doubles, the cumulative average time per unitfalls to a fixed percentage (referred to as the learning rate) of theprevious average time.
Wrights Law:as cumulative output doubles, the cumulative average time per unitfalls to a fixed percentage (referred to as the learning rate) of theprevious average time.
As can be seen on the graph, eventually the curve becomes almosthorizontal when many units have been produced, as the learning effect islost and production time per unit becomes a constant.
Learning curve calculations
The learning curve effect can be calculated by:
- Method 1: set up a table and reduce the average time by the learning rate each time the output doubles.
- Method 2: using the formula y = axb

Both methods will give the same answer. However, the formula is quicker and easier to use in the exam.

 Test your understanding 6 - Method 1
Test your understanding 6 - Method 1
Assume that it has taken 400 direct labour hours to manufacture thefirst unit of a new product. As in the past for this business it isanticipated that a 75% learning curve will occur.
Required:
Set up a table showing:
- The average time taken for the 2nd and the 4th unit.
- The total time taken for 2 units and for 4 units.


 Test your understanding 7 - Method 2
Test your understanding 7 - Method 2
Using the information from the previous test yourunderstanding, use the formula to calculate the cumulative average timeto produce four units.


 Additional example on method 2
Additional example on method 2
Assume that it takes 400 direct labour hours to produce the first unit of a new product and an 85% learning curve applies.
Required:
Calculate the total time to produce the third unit.
Solution
- b = log(0.85)/ log 2
b = –0.0706/ 0.3010 = –0.234
- The cumulative average time to produce the first two units is
y = 400 × 2–0.234 = 340.1.
The total time to produce the first two units = 340.1 × 2 = 680.2 hours.
- The cumulative average time to produce the first three units is
y = 400 × 3–0.234 = 309.3.
The total time to produce the first three units = 309.3 × 3 = 927.9 hours.
- The time to produce the third unit = 927.9 — 680.2 = 247.7 direct labour hours.


 Test your understanding 8
Test your understanding 8
A Swiss watch making company wishes to determine the minimum priceit should charge a customer for a special order of watches. The customerhas requested a quotation for 10 watches (1 batch), but mightsubsequently place an order for a further 10. Material costs are $30 perwatch. It is estimated that the first batch of 10 watches will take 100hours to manufacture and an 80% learning curve is expected to apply.Labour plus variable overhead costs amount to $3 per hour. Setup costsare $1,000 regardless of the number of watches made.
Required:
(a) What is the minimum price the company should quote for the initial order if there is no guarantee of further orders?
(b) If the company was then to receive the follow-on order, what would the minimum price of this order be?
(c) What would be the minimum price if both orders were placed together?
(d) Having completed the initial orders for atotal of 20 watches (price at the minimum levels recommended in (a) and(b)), the company thinks that there would be a ready market for thistype of watch if it brought the unit selling price down to $45. At thisprice, what would be the profit on the first 140 ‘mass-production'watches (i.e. after the first 20 watches) assuming that marketing coststotalled $250?

Applications of the learning effect
- Pricing decisions: prices will be set too high if based on the costs of making the first few units.
- Work scheduling: less labour per unit will be required as more units are made. This may have management implications, e.g. workers may be laid off.
- Product viability: the viability of a product may change if a learning effect exists.
- Standard setting: if a product enjoys a learning effect but this effect is ignored, then the standard cost will be too high. The presence of a learning effect can also make standard setting difficult.
- Budgeting: the presence of a learning effect should be taken into account when setting budgets. For example, the labour budget may be reduced by a learning effect but working capital may be required sooner than expected.
The learning curve and the steady state
The learning effect will only apply for a certain range of production.
For example, machine efficiency may restrict further improvements or there may be go-slow arrangements in place.
Once the steady state is reached the direct labour hours will notreduce any further and this will become the basis on which the budget isproduced.

 Test your understanding 9
Test your understanding 9
The first batch of a new product took 20 hours to produce. The learning rate is 90%.
Required:
If the learning effect ceases after 72 batches (i.e. all subsequentbatches take the same time as the 72nd), how long will it take to make agrand total of 100 batches?

Limitations of the learning curve model
The model applies if:
- the process is labour intensive: modern manufacturing can be very machine intensive. The learning effect will not apply if machines limit the speed of labour.
- there are no breaks in production: a break in production may result in the learning effect being lost.
- the product is new: the introduction of a new product makes it more probable that there will be a learning effect.
- the product is complex: the more complex the product, the more probable that the learning effect will be significant and the longer it will take for the learning effect to reach the steady state.
- the process is repetitive: if the process is not repetitive, a learning effect will not be enjoyed.
It may also be difficult to identify the learning effect in practice.

 The experience curve
The experience curve
It has been stressed that the learning curve was derived fromobservations of the reductions in direct labour time taken to completesuccessive repetitive but complex assembly tasks. However, learningrates have frequently been determined by fitting curves to total costper unit data. For example, DePuy (1993) used this method to ascertainfor the US government the learning rate achieved by defence contractors.The purpose in gathering this data was to help in price negotiationswith the contractors.
The slope of the learning curves derived ranged from 0.718 to1.021, with a mean of 0.858. These data suggest that defence contractorstypically enjoy a reduction of 14 per cent of average unit cost on eachdoubling of output. The strict application of the learning curvephenomenon is seen in the area of direct labour, and it is arguablethat, in using unit cost data, the result outlined above actuallyreflects the so-called ‘experience curve; rather than the learningcurve as strictly defined. The ‘experience curve' extends the learningcurve approach to areas other than direct labour. Rather than relatingindirectly to cost via time, an experience curve relates directly tocost, and it is a function which shows how total cost per unit declinesas output increases.
Total cost in experience curves includes all overhead types –production, marketing and distribution – and thus cost reductionarising from factors such as factory size, production technology,substitution of materials and design modifications are reflected in anexperience curve.
Experience curves, like learning curves, can be regarded asstatements of what will happen in practice. This could be considered tobe a western approach. An alternative approach, adopted by the Japanese,is that these curves should be taken as expressions of what isdesirable, and hence what should be striven for.
The improvement-oriented Japanese typically aim actively to foster a67 per cent learning curve, as against the 80 per cent curve moreusually found in the west.

7 Chapter summary
Test your understanding answers

 Test your understanding 1
Test your understanding 1
Step 1: Select the highest and lowest activity levels and their costs

Step 2: Find the variable cost per unit
Variable cost per unit = $240/120 = $2 per unit
Step 3: Find the fixed cost
Fixed inspection costs are, therefore:
$2,400 — (420 units × $2) = $1,560 per month
or $2,160 — (300 units × $2) = $1,560 per month
i.e. the relationship is of the form y = $1,560 + $2x.
Step 4: Use these costs to forecast the total costs for 500 units.
Total cost = fixed cost + variable cost
Total cost = $1,560 + ($2 × 500)
Total cost = $2,560


 Test your understanding 2
Test your understanding 2
(a)
There appears to be a positive linear relationship betweenadvertising expenditure and sales. The values of 'a' and 'b' can befound using the formulae.
(b)
b = ((6 × 60,600) – (240 × 1,440)) ÷ ((6 × 10,600) – 2402) = 18,000 ÷ 6,000 = 3
a = (1,440 ÷ 6) – (3 × (240 ÷ 6)) = 120
This means that when advertising expenditure is zero, sales will be$120,000, and for every $1 spent on advertising, sales will increase by$3.
(c) Line is: y = 120 + 3x
| (d) | (i)Advertising is $50,000 x = 50; y = 120 + (3 × 50) = 270 Forecast sales are $270,000 This is an interpolation, i.e. the value for advertising spend is within the sample range of values and is likely to be fairly accurate. (ii) Advertising is $100,000 x = 100; y = 120 + (3 × 100) = 420 Forecast sales are $420,000 This is an extrapolation, i.e. the value for advertising spend is outside the sample range and may be inaccurate. |


 Test your understanding 3
Test your understanding 3
(a)y = 150 + 10x
The 150 represents the trend when x = 0, i.e. the final quarter of 20X1.
The 10 represents the increase in trend each quarter, that is we expect the trend to rise by 10 each quarter.
The seasonal indices can be interpreted as follows:
Quarter 1 = 80. This means that we expect sales to be 80% of the trend value, i.e. 20% below the trend in quarter 1.
Quarter 2 = 110. This means that we expect sales to be 10% above the trend in quarter 2.
Quarter 3 = 140. This means that we expect sales to be 40% above the trend in quarter 3.
Quarter 4 = 70. This means that we expect sales to be 30% below the trend in quarter 4.
(b) and (c)
(d)The two main factors that may cause errors are:
(1) Extrapolation error – we may be forecasting too far beyond the original regression.
(2) We are ignoring any residual variation and cyclical variation. As a result, the forecast may be inaccurate.


 Test your understanding 4
Test your understanding 4

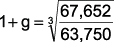
1 + g = 1.020
g = 0.020 = 2.0%


 Test your understanding 5
Test your understanding 5
- The expected value of sales revenue = ( 100,000 × 0.1) + (125,000 × 0.6) + (140,000 × 0.3) = $127,000
- This can be used as the sales figure in the budget.


 Test your understanding 6 - Method 1
Test your understanding 6 - Method 1

Once 2 units have been produced, and the learning processcontinues, the production of 2 more units will take only (900 – 600),i.e. 300 hours. This represents 150 hours per unit.


 Test your understanding 7 - Method 2
Test your understanding 7 - Method 2


 Test your understanding 8
Test your understanding 8
(a) Initial order

Note: If there is no guarantee of a follow-up order, the setup costs must be recovered on the initial order.
(b) Follow-on order
- b = log 0.8/ log 2 = – 0.321928
- If production increases to 20 watches (2 batches) then the cumulative average time per batch is:
y = axb
y = 100 × 2 -0.321928
y = 80.00 hours
- i.e. cumulative time for 20 watches (2 batches) = 160 hours
- Therefore, the time taken for the second batch of ten watches = 160 – 100 = 60 hours.
Costs are therefore:

Note: the set up costs have been recovered on the initial order and can therefore be ignored.
(c) Both orders together
Total costs are:

Note: This is the mean of the two previous prices.
(d) Mass production
- Total production = 20 watches for the special order + 140 watches for mass production = 160 watches or 16 batches.
- y = axb
Average time/batch for first 2 batches (i.e. first 20 watches)
= 100 × 2–0.3219 = 80 hours
Total time for first 2 batches = 80 × 2 = 160 hours (as before).
- Average time per batch for first 16 batches (i.e. first 160 watches) = 100 × 16–0.321928 = 40.96 hours.
Total time for first 16 batches = 40.96 × 16 = 655.36 hours.
Hence total time for batches 3 to 16 (i.e. the 140 mass-produced units) = (655.36 — 160) hours = 495.36 hours.
Cost of first 140 mass-production models:



 Test your understanding 9
Test your understanding 9
Step 1: Calculate the cumulative average time for the number of units/ batches at which the learning effect ceases.
b = log 0.9/log 2 = –0.152003
y = axb
Cumulative average time for 72 batches, y is:
y = 20 ×72–0.152003 = 10.44 hrs/batch
Step 2: Calculate the cumulative average time for the number of units/ batches, at which the learning effect ceases, minus 1
x = 71 batches
y = 20 × 71–0.152003 = 10.46 hrs/batch
Step 3: Calculate the time taken to make the unit/ batch at which the learning effect ceases.

Step 4: Calculate the total time for the number of units/batches
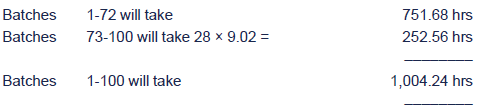

|
Created at 5/24/2012 4:41 PM by System Account
(GMT) Greenwich Mean Time : Dublin, Edinburgh, Lisbon, London
|
Last modified at 5/25/2012 12:54 PM by System Account
(GMT) Greenwich Mean Time : Dublin, Edinburgh, Lisbon, London
|
|
|
|
 |
Rating
:
|
 Ratings & Comments
(Click the stars to rate the page) Ratings & Comments
(Click the stars to rate the page)
|
 |
Tags:
|
|
|
|
|