Black Scholes option pricing model

Options are a key tool to assist financial risk management.

Options give the right but not the obligation to fix the price of a future transaction, thus enabling the owner of the option to protect themselves against adverse price movements but benefit from favourable ones. The resulting asymmetric risk exposure has value as indicated by the fact that a premium must be paid to acquire an option, whether or not it is ultimately exercised.

 The Black Scholes option pricing model is a method for determining the value / premium for European call options, although in some cases it can be adapted for other options as well.

Option terminology

The determinants of option value

The key aspect to an option's value is that the buyer has a choice whether or not to use it. Thus the option can be used to avoid downside risk exposure without foregoing upside exposure.

The value of an option is made up of two components. These are illustrated below for a call option:

The intrinsic value

The intrinsic value looks at the exercise price compared with the price of the underlying asset.

The value of the call option will increase as the share price increases. Conversely a lower exercise price would also give a higher option value.

An option can never have a negative intrinsic value. If the option is out of the money, then the intrinsic value is zero.

On the expiry date, the value of an option is equal to its intrinsic value.

The time value

The time value is derived from three elements:

Time to expiry.

• As the period to expiry increases, the chance of a profit before the expiry date grows, increasing the option value.

Volatility of the share price.

• The holder of a call option does not suffer if the share price falls below the exercise price, i.e. there is a limit to the downside.
• However the option holder gains if the share price increases above the exercise price, i.e. there is no limit to the upside.
• Thus the greater the volatility the better, as this increases the probability of a valuable increase in share price.

Risk-free interest rate.

• As stated above, the exercise price has to be paid in the future, therefore the higher the interest rates the lower the present value of the exercise price. This reduces the cost of exercising and thus adds value to the current call option value.
• Alternatively, since having a call option means that the share purchase can be deferred, owning a call option becomes more valuable when interest rates are high, since the money left in the bank will be generating a higher return.

A similar argument can be applied to put options resulting in the following summary of how changes in the five inputs affect the value of the option:

The Black Scholes Option Pricing Model

The Black-Scholes model values call options before the expiry date and takes account of all five factors that determine the value of an option.

The Formula

Value of a call option = P_a N(d₁) - P_eN(d₂)e^-rt

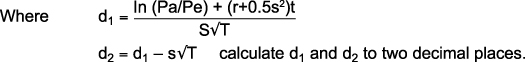
The key:

P_a = current price of underlying asset (e.g. share price)

P_e = exercise price

r = risk-free rate of interest

t = time until expiry of option in years

s = volatility of the share price (as measured by the standard deviation expressed as a decimal - see explanation below)

N(d) = equals the area under the normal curve up to d

e = 2.71828, the exponential constant

In = the natural log (log to be base e)

P_ee^-rt = present value of the exercise price calculated by using the continuous discounting factors.

Measures of volatility - standard deviation and variance

The measure of volatility used in the Black-Scholes model is the annual standard deviation (s), expressed as a decimal.

Exam questions may quote volatility in terms of the "variance",which is the square of the standard deviation. In this case, take the square root of the given variance figure to give the volatility in the correct terms for the Black-Scholes formula.

Alternatively, monthly, or weekly, standard deviations may be quoted. To convert from a monthly standard deviation to an annual figure,

• square the monthly standard deviation
• multiply by 12
• take the square root of the result.

This will now be the annual standard deviation figure as required

Underlying assumptions and limitations

The model assumes that:

• The options are European calls.
• There are no transaction costs or taxes.
• The investor can borrow at the risk-free rate.
• The risk-free rate of interest and the share's volatility is constant over the life of the option.
• The future share-price volatility can be estimated by observing past share price volatility.
• The share price follows a random walk and that the possible share prices are based on a normal distribution.
• No dividends are payable before the option expiry date.

In practice these unrealistic assumptions can be relaxed and the basic model can be developed to reflect a more complex situation.

Using the Black-Scholes model to value put options

If you have calculated the value of a call option using Black-Scholes, then the value of a corresponding put option can be found using the put call parity formula.

The put call parity equation is on the examination formula sheet:

Value of put P= c - P_a + P_e × e^-rt

Step 1: Value the corresponding call option using the Black-Scholes model.

Step 2: Then calculate the value the put option using the put call parity equation.

Application to American call options

One of the limitations of the Black-Scholes formula is that it assumes that the shares will not pay dividends before the option expires. If this holds true then the model can also be used to value American call options.

In fact, if no dividends are payable before the option expiry date, the American call option will be worth the same as a European call option. The reason for this is because if the American option-holder exercises early he will forfeit the time value of the option and simply realise the intrinsic value. Quite simply the option is worth more alive than dead. The right to exercise an American call early is irrelevant and the option will be exercised on the expiry date just like a European option.

Application to shares where dividends are payable before the expiry date

The Black-Scholes formula can be adapted to call options with dividends being paid before expiry by calculating a "dividend adjusted share price":

• Simply deduct the present value of dividends to be paid (before the expiry of the option) from the current share price.
• P_a, becomes P_a - PV (dividends) in the Black-Scholes formula

Delta and other "Greeks"

Delta and delta hedges

The figure N(d₁) is known as delta. Delta measures the change in option value which would result from a $1 change in the value of the underlying asset (e.g. share).

An investor can eliminate the risk of his shareholding by constructing a "delta hedge".

• An investor who holds a number of shares and sells (an option writer) a number of call options in the proportion dictated by the delta/the hedge ratio ensures a hedged portfolio. N.B. A hedged portfolio is one where the gains and losses cancel out against each other.
• Number of option calls to sell = Number of shares held/N(d₁).
• Alternatively, if you have already written call options, then a delta hedge can be constructed by buying shares.
• Number of shares to hold = Number of call options sold × N(d₁).

Because share prices change continuously in the real world, the value of delta also changes continuously. Therefore, the investor who wants to maintain a risk neutral position will have to continuously adjust the balance of options and shares in his portfolio. This process is known as "dynamic delta hedging".

Gamma, vega, rho and theta

Delta measures the sensitivity of the option value to changes in the value of the underlying asset (explained in detail above).

Sensitivities to other factors in the Black Scholes formula are denoted by other Greek letters as follows:

Gamma - measures the rate of change of delta as the underlying asset's price changes.

Vega - measures the change in option value caused by a 1% change in the volatility.

Rho - measures the sensitivity of the option value to changes in the risk free rate of interest.

Theta - measures the rate of decline in the value of the option caused by the passage of time.

Further areas of application

The BSOP formula can also be adapted for use in the following scenarios:

Real options

Flexibility adds value to an investment. Real options theory attempts to classify and value flexibility in general by taking the ideas of financial options pricing and developing them. Real options can be explored here.

Valuing shares

Because of limited liability, shareholders can walk away from a company when the debt exceeds the asset value. However, when the assets exceed the debts, those shareholders will keep running the business, in order to collect the surplus.

Therefore, the value of shares can be seen as a call option owned by shareholders - we can use Black-Scholes to value such an option. This can be explored in more detail here.

Determining credit spreads

For any bond the lender's required/expected return will be made up of two elements:

• The risk free rate of return
• A premium (the credit spread) based on the expected probability of default and the expected loss given default

Option pricing theory (OPT) can be used to calculate these credit spreads and the risk of default. This is covered in more detail here.

Determining the drivers of option value in practice

Value of the underlying asset

• For quoted underlying assets a value can be looked up on the market. Most markets give prices for buying and selling the underlying asset. A mid-price is usually used for option pricing.

  For example, if a price is quoted as 243 - 244 cents, then a mid-price of 243.5 cents should be used.

• In the case of unquoted underlying assets a separate exercise must be undertaken to value them.

  For example, suppose an unquoted company has issued share options to employees as part of their remuneration package. To value these call options (e.g. for disclosure or taxation purposes) one must first value the shares using, e.g. P/E ratios.

Exercise price and time to expiry

Both the exercise price and expiry date are stated in the terms of the option contract.

Volatility

• Volatility represents the standard deviation of day-to-day price changes in a security, expressed as an annualised percentage. Two measures of volatility are commonly used in options trading: historical and implied.
• Historical volatility can be measured by observing price changes of a security over a period of time. It is not necessarily a forecast of future volatility, but can be used to determine the option price.
• Implied volatility can be calculated by taking current quoted options prices and working backwards.

A common approach to calculating historical volatility is as follows:

(1) Calculate the daily return using (current price/previous days price) or P_n/P_n-1.

(2) Take the log of each return to convert into a continuous return.

(3) Calculate the standard deviation of the logs to get a daily volatility.

(4) Annualise the result.

Volatility calculation

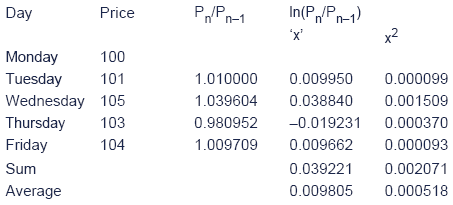
In order to calculate the volatility (standard deviation) we need to use these two final figures.

Volatility = square root of (the average value of x² less the square of the average value of x)

= Square root of (0.000518 - 0.009805²)

= 0.0205 or approximately 2%

Assuming 260 trading days on the market, Annualised volatility = daily volatility × 260^0.5 = 0.33 or 33%.

The method for calculating the continuous return in the above example may be unfamiliar to you. The basic idea is that instead of dividing a time period into years or weeks or days for discounting purposes we can discount continuously. To get the same answer either way, we need to set continuous rate = ln (1 + discrete rate)

For example, if the discrete rate is 10% p.a., then a continuous rate is given by

Continuous rate = ln1.10 = 0.0953 or 9.53%.

Discount factors using continuous rates are given by DF = e^-it where i is the continuous rate and t the time period.

Risk-free rate

• The risk-free rate is the minimum return required by investors from a risk-free investment.
• Treasury bills or other short-term (usually three months). Government borrowings are regarded as the safest possible investment and their rate of return is often given in a question to be used as a figure for the risk-free rate.

Rating :	Ratings & Comments  (Click the stars to rate the page)

Tags:	Black Scholes;options;option pricing;option value