Economic Order Quantity (EOQ)

The challenge of of good inventory management is to determine:

• the optimum re-order level (how many items are left in inventory when the next order is placed), and
• the optimum re-order quantity (how many items should be ordered when the order is placed)

In practice, this means striking a balance between holding costs on the one hand and stockout and re-order costs on the other. The economic order quantity formula is one approach to striking this balance.

Economic order quantity (EOQ)

For businesses that do not use just in time (JIT) inventory management systems, there is an optimum order quantity for inventory items, known as the EOQ.

The aim of the EOQ model is to minimise the total cost of holding and ordering inventory. To do this, it is necessary to balance the relevant costs. These are:

Holding costs

The model assumes that it costs a certain amount to hold a unit of inventory for a year (referred to as C_H in the formula). Therefore, as the average level of inventory increases, so too will the total annual holding costs incurred.

When new batches or items of inventory are purchased or made at periodic intervals, the inventory levels are assumed to exhibit the following pattern over time.

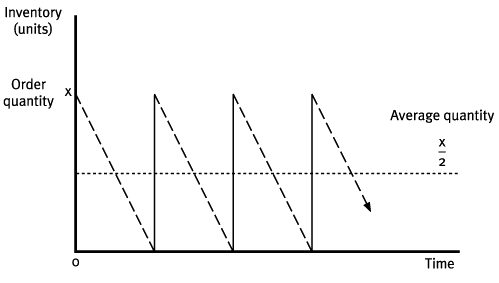
If x is the quantity ordered, the annual holding cost would be calculated as:

Holding cost per unit × Average inventory:

We therefore see an upward sloping, linear relationship between the re-order quantity and total annual holding costs.

Ordering costs

The model assumes that a fixed cost is incurred every time an order is placed (referred to as C_Oin the formula). Therefore, as the order quantity increases, there is a fall in the number of orders required, which reduces the total ordering cost.

If D is the annual expected sales demand, the annual order cost is calculated as:

Order cost per order × no. of orders per annum.

However, the fixed nature of the cost results in a downward sloping, curved relationship.

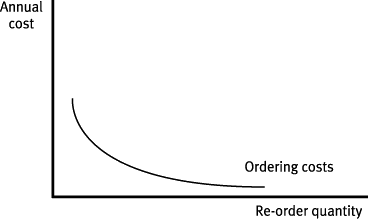
Balance between holding costs and ordering costs

Because you are trying to balance these two costs (one which increases as re-order quantity increases and one which falls), total costs will always be minimised at the point where the total holding costs equals the total ordering costs. This point will be the economic order quantity (EOQ).

Assumptions

The following assumptions are made:

• demand and lead time are constant and known
• purchase price is constant
• no buffer inventory held (not needed).

The calculation

The EOQ can be more quickly found using a formula:

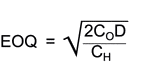
where:

C_O = cost per order

D = annual demand

C_H = cost of holding one unit for one year.

Quantity discounts

Discounts may be offered for ordering in large quantities. If the EOQ is smaller than the order size needed for a discount, companies must calculate if the order size should be increased above the EOQ.

The total inventory cost for the annual level of demand (including holding costs, ordering costs and purchase costs) should be compared:

• assuming the EOQ is used
• assuming the order size enabling the discount is used

The assumption is that the company would accept the discount and order in the larger quantity if the overall inventory cost is lower.

Rating :	Ratings & Comments  (Click the stars to rate the page)

Tags:	inventory management;EOQ;economic order quantity;holding costs;ordering costs