Duration

Duration is a concept that is used in investment appraisal as a way of measuring and incorporating risk. In practice it is commonly used to analyse corporate bonds.

Duration

Introduction to the concept of duration

Duration measures the average time to recover the present value of the project (if cash flows are discounted at the cost of capital).

Duration captures both the time value of money and the whole of the cash flows of a project. It is also a measure which can be used across projects to indicate when the bulk of the project value will be captured.

Projects with higher durations carry more risk than projects with lower durations.

The differences between Payback, Discounted Payback and Duration

Payback, discounted payback and duration are three techniques that measure the return to liquidity offered by a capital project.

In theory, a firm that has ready access to the capital markets should not be concerned about the time taken to recapture the investment in a project. However, in practice managers prefer projects to appear to be successful as quickly as possible.

Payback period

Payback as a technique fails to take into account the time value of money and any cash flows beyond the project date. It is used by many firms as a coarse filter of projects and it has been suggested to be a proxy for the redeployment real option.

Discounted payback period

Discounted payback does surmount the first difficulty but not the second in that it is still possible for projects with highly negative terminal cash flows to appear attractive because of their initial favourable cash flows. Conversely, discounted payback may lead a project to be discarded that has highly favourable cash flows after the payback date.

Duration

Duration measures either the average time to recover the initial investment (if discounted at the project's internal rate of return) of a project, or to recover the present value of the project if discounted at the cost of capital. Duration captures both the time value of money and the whole of the cash flows of a project. It is also a measure which can be used across projects to indicate when the bulk of the project value will be captured.

Its disadvantage is that it is more difficult to conceptualise than payback and may not be employed for that reason.

Calculation of duration

There are several different ways of calculating duration, the most common of which is Macauley duration, illustrated below.

A project with the following cash flows is under consideration:

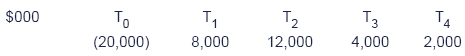
Cost of capital 8%

Required:

Calculate the project's Macauley duration.

Solution

The Macauley duration is calculated by first calculating the discounted cash flow for each future year, and then weighting each discounted cash flow according to its time of receipt, as follows:

Next, the sum of the (PV × Year) figures is found, and divided by the present value of these "return phase" cash flows.

Sum of (PV × Year) figures = 7,408 + 20,568 + 9,528 + 5,880 = 43,384

Present value of return phase cash flows = 7,408 + 10,284 + 3,176 + 1,470 = 22,338

Hence, the Macauley duration is 43,384 / 22,338 = 1.94 years

Benefits and limitations of duration

Benefits

Duration allows bonds of different maturities and coupon rates to be compared. This makes decision making regarding bond finance easier and more effective.

If a portfolio of bonds is constructed based on weighted average duration, it is possible to identify the change in value of the portfolio as interest rates change.

Managers may be able to reduce interest rate risk by changing the overall duration of the bond portfolio (e.g. by adding shorter maturity bonds to reduce duration).

Limitations

The main limitation of duration is that it assumes a linear relationship between interest rates and bond price. In reality, the relationship is likely to be curvilinear. The extent of the deviation from a linear relationship is known as convexity. The more convex the relationship between interest rates and bond price, the more inaccurate duration is for measuring interest rate sensitivity.

Further information on convexity

The sensitivity of bond prices to changes in interest rates is dependent on their redemption dates. Bonds which are due to be redeemed at a later date are more price-sensitive to interest rate changes, and therefore are riskier.

Duration measures the average time it takes for a bond to pay its coupons and principal and therefore measures the redemption period of a bond. It recognises that bonds which pay higher coupons effectively mature sooner compared to bonds which pay lower coupons, even if the redemption dates of the bonds are the same. This is because a higher proportion of the higher coupon bond's income is received sooner. Therefore these bonds are less sensitive to interest rate changes and will have a lower duration.

Duration can be used to assess the change in the value of a bond when interest rates change using the following formula:

ΔP = [-D × Δi × P]/[1 + i],

where P is the price of the bond, D is the duration and i is the redemption yield.

However, duration is only useful in assessing small changes in interest rates because of convexity. As interest rates increase, the price of a bond decreases and vice versa, but this decrease is not proportional for coupon paying bonds, the relationship is non-linear. In fact, the relationship between the changes in bond value to changes in interest rates is in the shape of a convex curve to origin, see below.

Duration, on the other hand, assumes that the relationship between changes in interest rates and the resultant bond is linear.

Therefore duration will predict a lower price than the actual price and for large changes in interest rates this difference can be significant. Duration can only be applied to measure the approximate change in a bond price due to interest changes, only if changes in interest rates do not lead to a change in the shape of the yield curve. This is because it is an average measure based on the gross redemption yield (yield to maturity). However, if the shape of the yield curve changes, duration can no longer be used to assess the change in bond value due to interest rate changes.

Rating :	Ratings & Comments  (Click the stars to rate the page)

Tags:	duration;macauley duration;discounted payback;payback period;investment appraisal;convexity