The High Low method

Hi-low is linked to the idea of cost behaviour and is one method for splitting semi-variable costs into their fixed and variable elements.

Making a distinction between fixed and variable costs in a semi-variable cost might be used:

• in product costing
• to analyse profitability of a product or department
• to help managers to make decisions about increasing/decreasing activity levels
• to estimate future costs (forecasting and budgeting)
• to estimate what costs should have been (for budgetary control and performance assessment).

The High Low method

The total cost of a semi-variable cost can be shown as:

Total costs = Total fixed costs + (Variable costs × Activity level)

To separate the fixed cost element from the variable cost element the high low method can be used.

Step 1

Select the highest and lowest activity levels, and their associated costs. (Note: do not take the highest and lowest costs)

Step 2

Calculate the variable cost per unit:

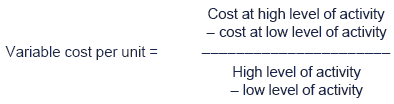
Step 3

Calculate the fixed cost by substitution, using either the high or low activity level.

Fixed cost = Total cost at activity level - Total variable cost

Step 4

Use the total fixed cost and the variable cost per unit values (steps 2 and 3) to calculate the estimated cost at different activity levels

Illustration - Applying the high low method

Assumptions

Assumptions of the high low method are as follows:

• the cost under consideration is potentially semi-variable (i.e. it has both fixed and variable elements)
• the linear model of cost behaviour is valid i.e. y = a + bx

High low method with stepped fixed costs

Sometimes fixed costs are only fixed within certain levels of activity and increase in steps as activity increases (i.e. they are stepped fixed costs).

• The high/low method can still be used to estimate fixed and variable costs. Simply choose 2 activity levels where the fixed cost remains unchanged.
• Adjustments need to be made for the fixed costs based on the activity level under consideration.

Illustration - high low with stepped fixed costs

An organisation has the following total costs at three activity levels:

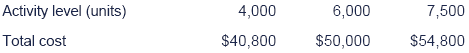
Variable cost per unit is constant within this activity range and there is a step up of 10% in the total fixed costs when the activity level exceeds 5,500 units.

What is the total cost at an activity level of 5,000 units?

Calculate the variable cost per unit by comparing two output levels where fixed costs will be the same:

Variable cost per unit = [(54,800 - 50,000) / (7,500 - 6,000)] = $3.20

Total fixed cost above 5,500 units = [54,800 - (7,500 x 3.20)] = $30,800

Total fixed cost below 5,500 units = 30,800/110 x 100 = $28,000

Total cost for 5,000 units = [(5,000 x 3.20) + 28,000] = $44,000

High low method with changes in the variable cost per unit

Sometimes there may be changes in the variable cost per unit, and the high low method can still be used to determine the fixed and variable elements of semi-variable costs by choosing 2 activity levels where the variable cost per unit remains unchanged.

Illustration - High low with variable cost changes

The following information relates to the manufacture of Product LL in 20X8:

For output volumes above 350 units the variable cost per unit falls by 10%. (Note: this fall applies to all units - not just the excess above 350).

Estimate the cost of producing 450 units of Product LL in 20X9.

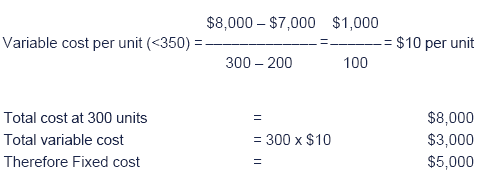
If output is 450 units in 20X9:

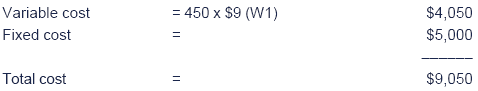
(W1) Variable cost per unit in 20X9 (when output > 350 units) = $10 x 0.9 = $9 per unit

Rating :	Ratings & Comments  (Click the stars to rate the page)

Tags:	hi-low;semi-variable costs