Linear Programming

Linear programming is a technique for decision making in the context of two or more scarce resources. If only one resource is in short supply then key factor analysis is the preferred method.

Formulating a linear programming problem involving two variables

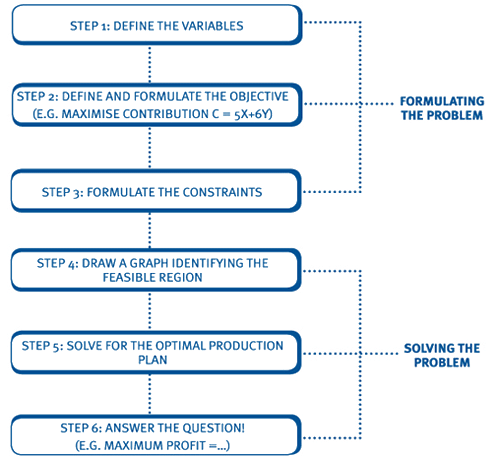
The steps involved in linear programming are as follows:

Illustration

A company produces two products in three departments. Details are shown below regarding the time per unit required in each department, the available hours in each department and the contribution per unit of each product: 

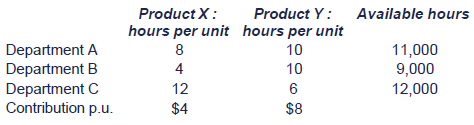
A step-by-step approach to determine what the optimum production plan is can be presented as follows :

Step 1 : Define the variables

Let 'x' be the number of units of X to produce; Let 'y' be the number of units of Y to produce.

Step 2 : Define and formulate the objective function

Objective function: to maximise contribution C= $4x + $8y

Step 3 : Formulate the constraints

Subject to:
In Department A, 8x + 10y ≤ 11,000 hours
In Department B, 4x + 10y ≤  9,000 hours
In Department C, 12x +  6y ≤ 12,000
x,y≥0

Step 4 : Draw a graph identifying the feasible region 

To draw Constraint 1 (constraint in Department A), we take the inequality '8x + 10y ≤ 11,000 hours' and turn it into an equation : 8x+ 10y = 11,000.

To draw this constraint, we need two points. If X = 0, Y = 11,000· 10 so Y = 1,100. Likewise, if Y = 0, X = 11,000 so X = 1,375.

To draw Constraint 2 (Department B) : If X = 0, Y = 900 and if Y = 0, X = 2,250.

To draw Constraint 3 (Department C) : If X = 0 , Y = 2,000 and if Y = 0, X = 1,000

Step 5 : Finding the optimum solution - Using the isocontribution line

We do not know the maximum value of the objective function;however, we can draw an isocontribution (or 'profit') line that shows all the combinations of x and y that provide the same total value for the objective function.

If, for example, we need to maximise Contribution $4x + $8y, we can draw a line on a graph that shows combination of values for x and y that give the same total contribution, when x has a contribution of $4 and y has a contribution of $8.

Any total contribution figure can be picked, but a multiple of $4 and $8 is easiest.

• For example, assume 4x + 8y = 4,000. This contribution line could be found by joining the points on the graph x = 0, y = 500 and x = 1,000 and y = 0.
• Instead, we might select a total contribution value of 4x + 8y = $8,000.This contribution line could be found by joining the points on the graph x = 0, y = 1,000 and x = 2,000 and y = 0.
• When drawing both of these contribution lines on a graph, we find that the two lines are parallel and the line with the higher total contribution value for values x and y ($8,000) is further away from the origin of the graph (point 0).
• This can be used to identify the solution to a linear programming problem. Draw the isocontribution line showing combinations of values for x and y that give the same total value for the objective function.
• Look at the slope of the contribution line and, using a ruler, identify which combination of values of x and y within the feasible area for the constraints is furthest away from the origin of the graph. This is the combination of values for x and y where an isocontribution line can be drawn as far to the right as possible that just touches one corner of the feasible area. This is the combination of values of x and y that provides the solution to the linear programming problem.

Optimum corner is Corner C, the intersection of:

The optimum production plan is to produce 500 units of Product X and700 units of Product Y; The contribution at this point is maximised C =(500 x $4) + (700 x $8) = $7,600.

Discussion aspects

Assumptions

• There is a single quantifiable objective,e.g. maximise contribution. In reality there may be multiple objectives such as maximising return while simultaneously minimising risk.
• Each product always uses the same quantity of the scarce resource per unit. In reality this may not be the case. For example, learning effects may be enjoyed.
• The contribution per unit is constant. In reality this may not be the case:
  • the selling price may have to be lowered to sell more
  • there may be economies of scale, for example a discount for buying in bulk.
• Products are independent - in reality:
  • customers may expect to buy both products together
  • the products may be manufactured jointly together.
• The scenario is short term. This allows us to ignore fixed costs.

The assumptions apply to the analysis used when there is one limiting factor or if there are multiple limiting factors.

Slack

Slack is the amount by which a resource is under-utilised.It will occur when the optimum point does not fall on a given resource line.

Slack is important because unused resources can be put to another use, e.g. hired out to another manufacturer.

Shadow (or dual) prices

The shadow price of a resource can be found by calculating the increase in value (usually extra contribution) which would be created by having available one additional unit of a limiting resource at its original cost.

• It therefore represents the maximum premium that the firm should be willing to pay for one extra unit of each constraint. This aspect is discussed in more detail below.
• Non-critical constraints will have zero shadow prices as slack exists already.

Calculating shadow prices

The simplest way to calculate shadow prices for a critical constraint is as follows:

Step 1: Take the equations of the straight lines that intersect at the optimal point. Add one unit to the constraint concerned, while leaving the other critical constraint unchanged.

Step 2: Use simultaneous equations to derive a new optimal solution

Step 3: Calculate the revised optimal Contribution. The increase is the shadow price for the constraint under consideration.

Implications of shadow prices

• Management can use shadow prices as a measure of the maximum premium that they would be willing to pay for one more unit of the scarce resource.
• However, the shadow price should be considered carefully. For example, the shadow price of labour may be calculated as $20 per hour. However, it may be possible to negotiate a lower shadow price than this.
• In addition, if more of the critical constraint is obtained, the constraint line will move outwards altering the shape of the feasible region. After a certain point there will be little point in buying more of the scarce resource since any non-critical constraints will become critical.

Rating :	Ratings & Comments  (Click the stars to rate the page)

Tags:	scarce resources;linear programming;slack;shadow prices;dual prices;constraints;objective function;iso-contribution line