Discount cash flow techniques
When appraising capital projects, basic techniques such as ROCE and Payback could be used. Alternatively, companies could use discounted cash flow techniques discussed on this page, such as Net Present Value (NPV) and Internal Rate of Return (IRR).
Cash flows and relevant costs
For all methods of investment appraisal, with the exception of ROCE, only relevant cash flows should be considered. These are:
-
cash flows that will happen in the future, and
-
cash flows that will arise only if the capital project goes ahead. future
The following should always be ignored in investment appraisal:

The time value of money
Money received today is worth more than the same sum received in the future, i.e. it has a time value.
This occurs for three reasons:
Discounted cash flow (DCF) techniques take account of this time value of money when appraising investments.
Compounding
A sum invested today will earn interest. Compounding calculates the future or terminal value of a given sum invested today for a number of years.
To compound a sum, the figure is increased by the amount of interest it would earn over the period.
Example of compounding:
An investment of $100 is to be made today. What is the value of the investment after two years if the interest rate is 10%?
Solution

The $100 will be worth $121 in two years at an interest rate of 10%.
Formula for compounding:
To speed up the compounding calculation, we can use a formula to calculate the future value of a sum invested now. The formula is:
F = P(1 + r)n
where F = Future value after n periods
P = Present or Initial value
r = Rate of interest per period
n = Number of periods
Discounting
In a potential investment project, cash flows will arise at many different points in time. To make a useful comparison of the different flows, they must all be converted to a common point in time, usually the present day, i.e. the cash flows are discounted.
The present value (PV) is the cash equivalent now of money receivable/payable at some future date.
Formula for discounting:
The PV of a future sum can be calculated using the formula:

This is just a re-arrangement of the formula used for compounding.
(1 + r)-n is called the discount factor (DF).
Example of discounting:
What is the PV of $115,000 receivable in nine years' time if r = 6%?
Solution:
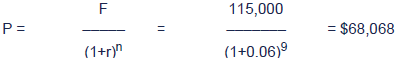
The cost of capital
In discounted cash flow techniques, the rate of interest is required. There are a number of alternative terms used to refer to the rate of interest:
-
cost of capital
-
discount rate
-
required return.
Different ways of determining a cost of capital are discussed here
Net Present Value (NPV)
To appraise the overall impact of a project using DCF techniques involves discounting all the relevant cash flows associated with the project back to their PV (present value).
If we treat outflows of the project as negative and inflows as positive, the NPV of the project is the sum of the PVs of all flows that arise as a result of doing the project.
Decision rule:
The NPV represents the surplus funds (after funding the investment) earned on the project, therefore:
-
if the NPV is positive - the project is financially viable
-
if the NPV is zero - the project breaks even
-
if the NPV is negative - the project is not financially viable
-
if the company has two or more mutually exclusive projects under consideration it should choose the one with the highest NPV
Assumptions in calculating the net present value
The following assumptions are made about cash flows when calculating the net present value:
-
all cash flows occur at the start or end of a year
-
initial investments occur T0
-
other cash flows start one year after that (T1).
Also interest payments are never include within an NPV calculation as these are taken account of by the cost of capital.
Example using NPV
An organisation is considering a capital investment in new equipment. The estimated cash flows are as follows.

The company's cost of capital is 9%.
Calculate the NPV of the project to assess whether it should be undertaken.
Solution:
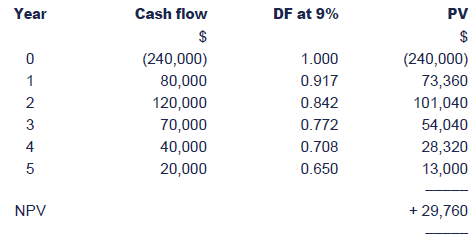
The PV of cash inflows exceeds the PV of cash outflows by $29,760,which means that the project will earn a DCF return in excess of 9%,i.e. it will earn a surplus of $29,760 after paying the cost of financing. It should therefore be undertaken.
Advantages and disadvantages of using NPV
Advantages
Theoretically the NPV method of investment appraisal is superior to all others. This is because it:
-
considers the time value of money
-
is an absolute measure of return
-
is based on cash flows not profits
-
considers the whole life of the project
-
should lead to maximisation of shareholder wealth.
Disadvantages
-
It is difficult to explain to managers
-
It requires knowledge of the cost of capital
-
It is relatively complex.
Calculating discount factors
Discount factors can always be calculated using the formula (1 + r)-n.
However in some special cases, time-saving techniques can be used.
Discounting annuities
An annuity is a constant annual cash flow for a number of years.
Where an investment appraisal involves a constant annual cash flow, a special discount factor known as an annuity factor can be used.
The annuity factor (AF) is the name given to the sum of the individual DF. The formula for the annuity factor is:
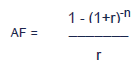
Example using annuity factor:
A payment of $3,600 is to be made every year for seven years, the first payment occurring in one year's time. The interest rate is 8%.What is the PV of the annuity.
Solution:
The AF can be found using the formula:
Therefore the PV of the annuity is $3,600 × 5.206 = $18,741.60
Discounting perpetuities
A perpetuity is an annual cash flow that occurs forever..
The PV of a perpetuity is found using the formula
cash flow
PV=_______
r
or
1
PV=cash flow x ____
r
1
___ is known as the perpetuity factor
r
Example using perpetuity factor:
What is the present value of $3,000 received in one year's time and for ever if the interest rate is 10%?
Solution:

Present Value Tables
(1 + r)-n is called the discount factor (DF). This can be found from the formula, or from special Present Value tables in which many discount factors have already been calculated. There are also Annuity Tables in which many annuity factors have already been calculated.
Advanced and delayed annuities and perpetuities
The use of annuity factors and perpetuity factors both assume that the first cash flow will be occurring in one year's time. Annuity or perpetuity factors will therefore discount the cash flows back to give the value one year before the first cash flow arose. For standard annuities and perpetuities this gives the present (T0) value since the first cash flow started at T1.
Be careful: if this is not the case, you will need to adjust your calculation.
In some investment appraisals, regular cash flows may start now (at T0) rather than in one year's time (T1).
Calculate the PV by ignoring the payment at T0 when considering the number of cash flows and then adding one to the annuity or perpetuity factor.
Example using advanced annuities
A 5-year $600 annuity is starting today. Interest rates are 10%. Find the PV of the annuity.
Solution
This is essentially a standard 4-year annuity with an additional payment at T0. The PV could be calculated as follows:
PV = 600 + 600 × 3.17 = 600 + 1902 = $2,502
The same answer can be found more quickly by adding 1 to the AF:
PV = 600 × (1 + 3.17) = 600 × 4.17 = $2,502.
Example using advanced perpetuities
A perpetuity of $2,000 is due to commence immediately. The interest rate is 9%. What is the PV?
Solution
This is essentially a standard perpetuity with an additional payment at T0. The PV could be calculated as follows:


Again, the same answer can be found more quickly by adding 1 to the perpetuity factor.
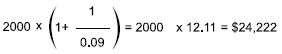
Delayed annuities and perpetuities
Some regular cash flows may start later than T1.
These are dealt with by:
(1)applying the appropriate factor to the cash flow as normal
(2)discounting your answer back to T0.
Example of delayed annuities
For delayed cash flows, applying the standard annuity factor will find the value of the cash flows one year before they began, which in this illustration is T2. To find the PV, an additional calculation is required the value must be discounted back to T0.
What is the PV of $200 incurred each year for four years, starting in three year's time, if the discount rate is 5%?
Solution


The Internal Rate of Return (IRR)
The IRR is another project appraisal method using DCF techniques.
The IRR represents the discount rate at which the NPV of an investment is zero. As such it represents a breakeven cost of capital.
Your FeedbackWe value your feedback on the topics or anything else you have found on our site, so we can make it even better.Give Feedback
Calculating the IRR using linear interpolation
The steps in linear interpolation are:
(1)Calculate two NPVs for the project at two different costs of capital
(2)Use the following formula to find the IRR:

where:
L = Lower rate of interest
H = Higher rate of interest
NL = NPV at lower rate of interest
NH = NPV at higher rate of interest.
The diagram below shows the IRR as estimated by the formula.
Decision rule:
Example using IRR
A potential project's predicted cash flows give a NPVof $50,000 at a discount rate of 10% and an NPV of $10,000 at a rate of 15%.
Calculate the IRR.
Solution:
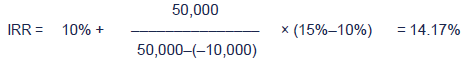
The IRR = 14.17%
Advantages and disadvantages of IRR
Advantages
The IRR has a number of benefits, e.g. it:
-
considers the time value of money
-
is a percentage and therefore easily understood
-
uses cash flows not profits
-
considers the whole life of the project
-
means a firm selecting projects where the IRR exceeds the cost of capital should increase shareholders' wealth.
Disadvantages
-
It is not a measure of absolute profitability.
-
Interpolation only provides an estimate and an accurate estimate requires the use of a spreadsheet programme.
-
It is fairly complicated to calculate.
-
Non-conventional cash flows may give rise to multiple IRRs which means the interpolation method can't be used.
Difficulties with the IRR approach
Interpolation only provides an estimate (and an accurate estimate requires the use of a spreadsheet programme). The cost of capital calculation itself is also only an estimate and if the margin between required return and the IRR is small, this lack of accuracy could actually mean the wrong decision is taken.
Another drawback of IRR is that non-conventional cash flows may give rise to no IRR or multiple IRRs. For example a project with an outflow at T0 and T2 but income at T1 could, depending on the size of the cash flows, have a number of different profiles on a graph (see below). Even where the project does have one IRR, it can be seen from the graph that the decision rule would lead to the wrong result as the project does not earn a positive NPV at any cost of capital.
NPV versus IRR
Both NPV and IRR are investment appraisal techniques which discount cash flows and are superior to the basic techniques such as ROCE or payback. However only NPV can be used to distinguish between two mutually-exclusive projects, as the diagram below demonstrates:
The profile of project A is such that it has a lower IRR and applying the IRR rule would prefer project B. However in absolute terms, A has the higher NPV at the company's cost of capital and should therefore be preferred.
NPV is therefore the better technique for choosing between projects.
The advantage of NPV is that it tells us the absolute increase in shareholder wealth as a result of accepting the project, at the current cost of capital. The IRR simply tells us how far the cost of capital could increase before the project would not be worth accepting.
The modified internal rate of return (MIRR) solves many of these problems with the conventional IRR.
|
Created at 9/5/2012 3:08 PM by System Account
(GMT) Greenwich Mean Time : Dublin, Edinburgh, Lisbon, London
|
Last modified at 11/1/2016 3:10 PM by System Account
(GMT) Greenwich Mean Time : Dublin, Edinburgh, Lisbon, London
|
|
|
|
 |
Rating
:
|
 Ratings & Comments
(Click the stars to rate the page) Ratings & Comments
(Click the stars to rate the page)
|
 |
Tags:
|
|