Using options to value credit spreads

 For any bond the lender's required/expected return will be made up of two elements:

• The risk free rate of return
• A premium (the credit spread) based on the expected probability of default and the expected loss given default Option pricing theory

  (OPT) can be used to calculate these credit spreads and the risk of default.

Overview of the method

A key concept in this context is that shareholders can be viewed as having a call option on the company's assets. By redeeming the debt, shareholders effectively acquire the assets of the company. Default hands the assets to the lenders.

Shareholders exercise this option if the value of the firm's assets is at least equal to the redemption value. If not, then the option is allowed to lapse, the company is handed over to the debt holders and the shareholders walk away.

Not defaulting thus corresponds to the call option being in the money at expiry.

(A corresponding view is that the lenders have sold a put option under which the company is sold to them for more than it's worth -they give up the full redemption value in exchange for the company assets)

Numerical illustration

Credit spreads

Suppose OPT Inc has the following capital structure

Furthermore, suppose that:

• The (discrete) risk-free rate r_f = 5%
• Volatility = s = 25%

Next, let us start by considering the case if the debt were risk free.

(1) The yield to the lender would be 5% and so the redemption value in 5 years should be 60 (1.05)⁵ = 76.577

(2) The equity can then be valued as a call option on the company's assets:

• Value of underlying asset = 100
• Exercise price = redemption value of debt = 76.577
• Volatility = s = 25%
• Continuous risk free rate = ln(1.05) = 0.04879 = 4.879%
• t = 5

Using this with the Black Scholes formula gives a call value of 44

(3) The current value of debt can then be valued as the total asset value less the value of the equity:

Value of debt = 100 - 44 = 56

This is the wrong answer as we know the debt to be worth 60.The problem is that lenders will require a risk adjusted return higher than 5% and hence a higher redemption value than 76.577

(4) Using the solver or goal-seek function in a spreadsheet software package this calculation can be reversed to determine what redemption value does give the current value of debt as 60. The required redemption value is 84.

The required return of the lender is thus given by

1 + r = (84/60)^1/5 = 1.07

The lender thus requires 7%, giving a credit spread of 2% over the risk free rate.

Note the return and spread have been calculated using discrete returns. A continuous approach would be as follows:

• Required return of lender = (1/5) × ln(84/60) = 0.06729 or 6.729%
• Credit spread = 0.06729 - 0.04879 = 0.0185 or 1.85%.

The probability of default

It can be shown that the probability of a call option ending in the money can be calculated as N(d*), where d* is given by

Where µ = (continuous return) on the company's assets

Suppose in our OPT Inc example that

• The (discrete) market return r_m = 9²/₃%
• Asset beta = β_a = 0.6

From this data we can use CAPM  to calculate a required return on the company's assets as

K_a = r_f + β_a(r_m - r_f) = 0.05 + 0.6(0.09666 - 0.05) = 0.078 or 7.8%

This can be converted into a continuous return as µ= ln(1.078) = 0.0751 or 7.51%

Substituting this into the above formula for d*:

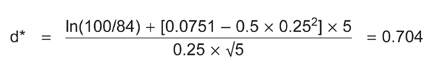
The probability of NOT defaulting is N(0.704) = 0.758

The probability of default is then 1 - 0.758 = 0.242 or 24.2%.

Rating :	Ratings & Comments  (Click the stars to rate the page)

Tags:	credit spreads;Black Scholes